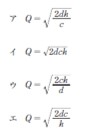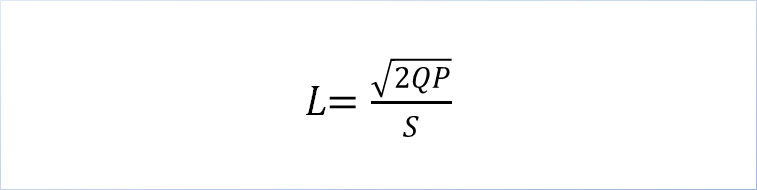標準400時間で「1次」を受かる時短が進む一方、「1次」知識をおろそかにうっかり「2次」を受けると確率8割でベテふぞループ。そこで「時間のかかる計算問題を後回し」にしたのは慧眼です。
「運営」計算問題には本試験90分ではとても解けない奇問が含まれ、ベテのようにムキになると沼ります。そこで同じ初見ドッキリな、中学入試「算数」を参考にします。
高校入試は受からせる試験で、中学入試は落とす試験。そこに飛び出す初見ドッキリ?
初見のドッキリ問題は、受験者が問題の本質を見極める能力を測るために使用されます。これらの問題は通常の問題とは異なる視点から提示されるため、受験者は問題の本質を理解し、根本的な考え方や計算手法を適用する必要があります。
同じく初見の問題は、過去問の答を完全にマスターした結果を適用するのではなく、新たな状況に適応する能力を測るために出題されます。これにより、受験者は柔軟性を発揮し、予期せぬ出題変化に対応する能力を向上させることができるのです。
初見のドッキリ問題はこのようにして、受験者の問題解決能力を向上させます。これらの問題は、電卓依存の計算お馬鹿に陥ることなく、論理的思考や創造性を駆使して問題を解決する機会を提供します。その結果、受験者はより幅広い視野で初見の事態に恐れず挑むマインドを鍛え、晴れて中小企業診断士を名乗ることを許されるのです。
おぉ、さすが同業D社が一生知らない所を5秒で答える生成AI。もし過去マス信者が計算問題ドリルに挑むなら、ご子息の中学入試問題集を借り、その角に頭をぶつけてやわらかくしてから解くのが吉な。
「生産管理」45マーク
生産方式&レイアウト
ライン生産→サイクルタイムの計算問題はこの科目で一番難しく、さらにスケジュール(PERT)の問題と混同させて苦手化を狙ってきます。正答率C以下=同業D社が解けない所なので、得意化するまで時間をかけます。
下線部は解答に使わないダミー条件。ここにハマって悩むとベテ化します。
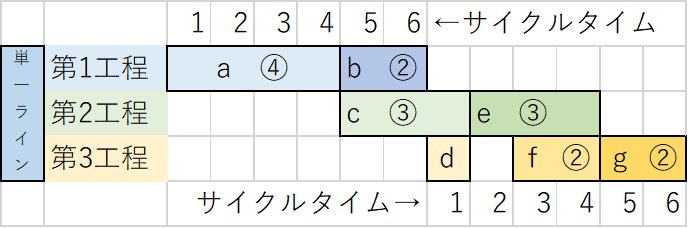
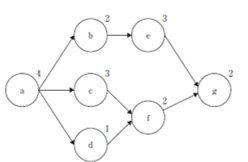
| 要素作業a~gの先行関係が下図に示される製品を、単一ラインで生産する。生産計画量が380 個、稼働予定時間が40 時間のとき、実行可能なサイクルタイムと最小作業工程数の組み合わせとして、最も適切なものを下記の解答群から選べ。 |
| サイクルタイム | 最小作業工程数 | |
| ○ア | 6分 | 3 |
| ×イ | 6分 | 4 |
| ×ウ | 9分 | 2 |
| ×エ | 9分 | 3 |
ライン編成効率=サイクルタイムに占める稼働時間の割合。設問文の下線部は計算に使わないダミー条件です。
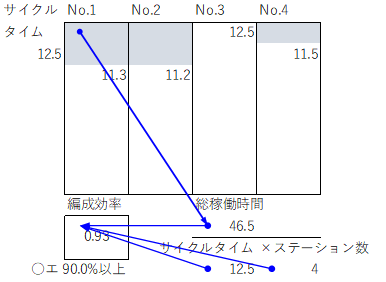
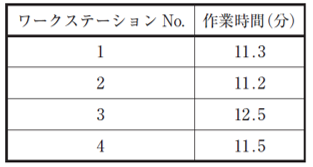
| ある単一品種ラインにおいて、1 か月864 個の生産を計画している。当該の計画生産能力を25 日/月、8 時間/日、稼働率90 %として作業編成を行った結果、下表となった。このときのライン編成効率の範囲として、最も適切なものを下記の解答群から選べ。 |
 |
| ×ア 70.0 %未満 ×イ 70.0 %以上80.0 %未満 ×ウ 80.0 %以上90.0 %未満 ○エ 90.0 %以上 |
(設問1)はやや難解で、サイクルタイム=5,900個を700hで作るには1hあたり8.4個から決めます(60分÷8.4=7.1分)。すると7分を超える×ウエオを外せるのでアイの2択にできます。
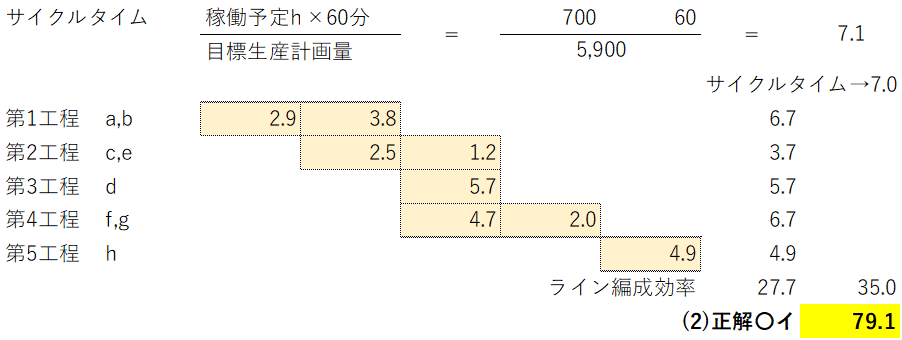
| (設問1) | 第1工程 | 第2〃 | 第3〃 | 第4〃 | 第5〃 |
| ×ア | a | b,c | d | e,h | f,g |
| 〇イ | a,b | c,e | d | f,g | h |
| ×ウ | a,b | c,f | d,e | g,h | - |
| ×エ | a,b,c | d,e,g | f,h | - | - |
| ×オ | a,b,c | d,g | c,f | h | - |
| 以下の文章を読んで、下記の設問に答えよ。 |
| 要素作業a~hの先行関係が下図に示される製品を単一ラインで生産する。稼働予定時間は700 時間で、目標生産計画量は5,900 個である。ただし、設定サイクルタイムは分単位の整数値とする。 |
計算は上図参照。サイクルタイム・編成効率は苦手にしやすいので、ここは後回しにして次のPERTを当てます。
| (設問2) 目標生産計画量を達成することを前提に、生産ラインの各工程に要素作業を割り付けた。その割り付けの組み合わせとして、最も適切なものはどれか。 |
| (設問2 ) 生産ラインの編成効率として、最も近い値はどれか(単位:%)。 ×ア 69 〇イ 79 ×ウ 89 ×エ 97 ×オ 99 |
サイクルタイムは、通学や通信でしっかり基礎を学ばないと間違いやすい、ド苦学トラップ問題です。エクセル図解を参照ください。
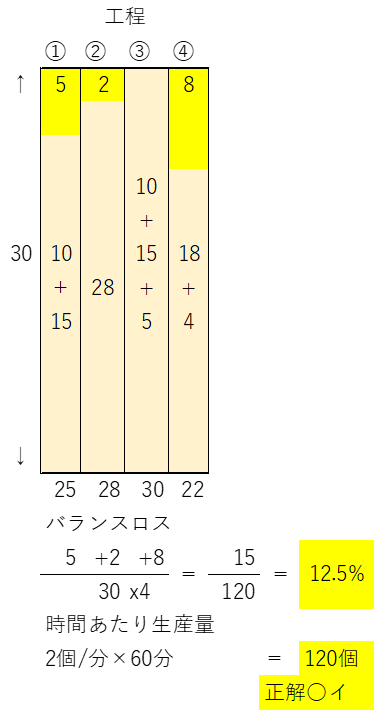
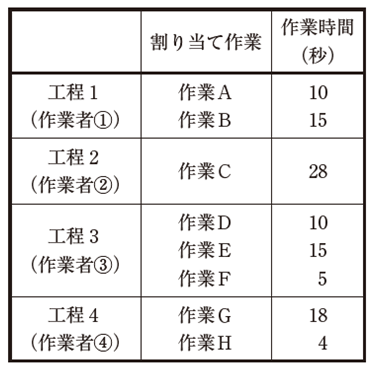
| 下表のように設定されたライン生産の状況から計算された、⒜バランスロスと⒝1 時間当たりの生産量の値(個)として、最も適切な組み合わせを下記の解答群から選べ。ただし、サイクルタイムは30秒とし、生産立ち上げ期間は考慮しない。 |
 |
| (a) | (b) | |
| ×ア | 12.5% | 30個 |
| ○イ | 12.5% | 120個 |
| ×ウ | 26.5% | 30個 |
| ×エ | 87.5% | 30個 |
| ×オ | 87.5% | 120個 |
当問もPERTとは別物で、サイクルタイムの出題です。本試験中に当てようとすると時間ロスするので、正解(ウ)と知ってから、本当にそうなるかをエクセルで確かめる。またR5第6問とセットにすると、バランスロス=14.3%も計算できます。
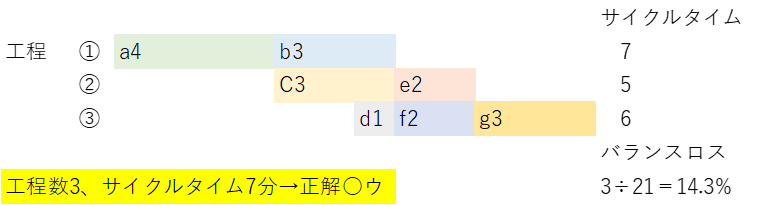
| 要素作業a~gの先行関係が下図に示される製品を、単一ラインで生産する。生産計画量が200 個、稼働予定時間が30 時間のとき、実行可能な最小の作業工程数とその工程数での最小のサイクルタイムの組み合わせとして、最も適切なものを下記の解答群から選べ。 |
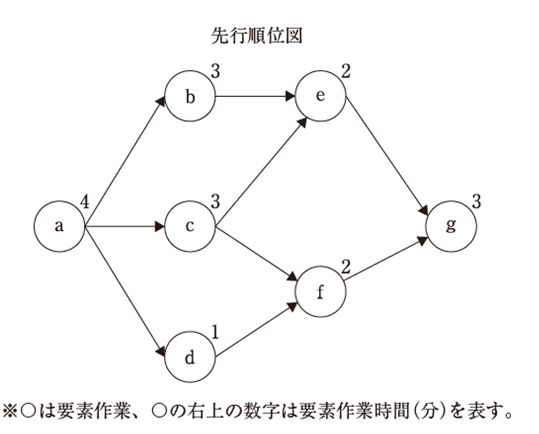 |
| 作業工程数 | サイクルタイム | |
| ×ア | 2 | 9分 |
| ×イ | 3 | 6分 |
| ○ウ | 3 | 7分 |
| ×エ | 3 | 8分 |
| ×オ | 4 | 5分 |
フロムトゥチャートの読み取りに関する基本問題です。正解に飛びつくのでなく、バツを全てマルに直して確実に当てます。
| × | →○ | |
| ×ア | D・F | C・D |
| ×イ | 他の | 機械ABを除く |
| ×エ | 12 | 14 |
| ×オ | C(49) | D(50) |
| ある工場の8 台の機械A~H間における1 日の品物の運搬回数を分析した結果、次のフロムツウチャートが得られた。この図表から読み取れる内容に関する記述として、最も適切なものを下記の解答群から選べ。 |
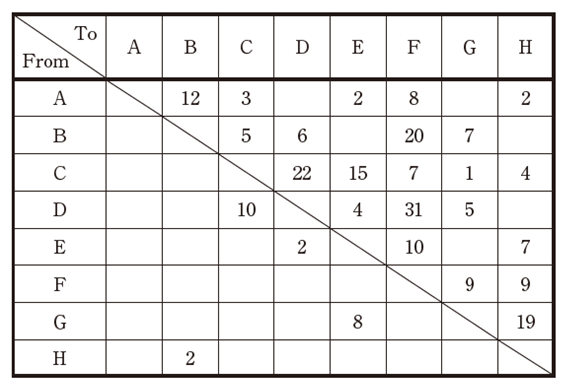 |
| ×ア 運搬回数が最も多いのは機械D・F間である。 ×イ 機械Cからは他のすべての機械に品物が運搬されている。 ○ウ 機械間で双方向の運搬が発生するのは2 カ所である。 ×エ 他の機械からの機械Bへの運搬回数は12 である。 ×オ 流出する運搬回数が最も多いのは機械Cである。 |
日程計画
日程計画の設問は、与えられた文章や値から図を描き起こし、周囲に説得する力を問う。論点こそ違いますが、ここをドリルすると「事例Ⅳ」CVPやNPVを得意化できます。
スケジュールを考える狙いは、【どの順序でやれば最短?】です。ジョブショップが個別生産、フローショップは連続ライン生産です。
ジョブショップ・スケジューリング
本来のジョブショップとは異なりますが、日程計画に関する良問。生産所要hが稼働hを超えているので、〇ア外注します。また、計算しなくてもイウエは×です。
| × | →○ | |
| ○ア | 一部作業の外注化を行う。 | |
| ×イ | 次期の仕事を前倒しして行う。 | 一部を翌期分納にできないか検討 |
| ×ウ | 終業時刻を早めて小集団活動を行う。 | 小集団活動を延期して残業を検討 |
| ×エ | 特別な施策は必要ない。 | ←欠品してそのまま失注リスク |

| ある工程における製品Aの1 個当たりの標準作業時間は0.3 時間で、適合品率は90 %である。この工程を担当する作業者は5 人で、1 人1 日当たりの実働時間は6時間、稼働率は90 %である。今期、残り10 日間に適合品を900 個生産しなければならないことが分かっている。 この場合にとるべき施策として、最も適切なものはどれか。 |
| 〇ア 一部作業の外注化を行う。 ×イ 次期の仕事を前倒しして行う。 ×ウ 終業時刻を早めて小集団活動を行う。 ×エ 特別な施策は必要ない。 |
ジョブショップでは、棒グラフ(ガントチャート)で試行錯誤しないと求まらないことがあり、難問になります。ここは最短で18hに。
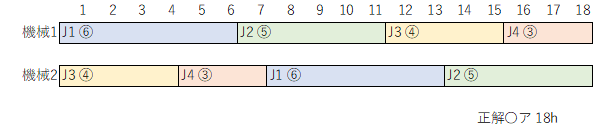
| 2 機械ジョブショップにおいて、各ジョブの作業時間と作業順序が下表に与えられている。各ジョブのジョブ投入順序をLPT(最長作業時間)ルールで決定したとき、総所要時間の値として最も適切なものを下記の解答群から選べ。 |
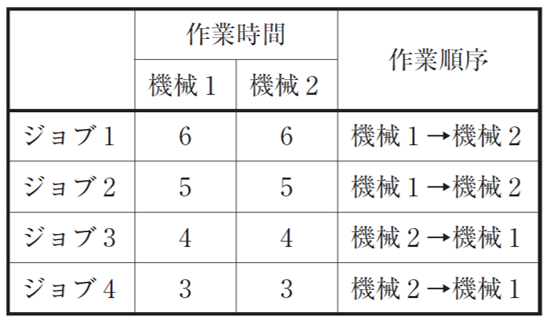 |
| 〇ア 18 ×イ 19 ×ウ 20 ×エ 21 ×オ 22 |
当問は一見×オ(納期が早い順)を選びたくなりますが、待ち時間が短い○イ(作業時間が短い順)が正解に。これも難問です。
| 下表の5つのJobが、ある1 つの設備で作業を実施されるために、順番に到着して待機している。ただし、納期は最初の作業を開始する時刻を起点とした値である。また、5つのJobは連続して処理される。 最初の作業が開始されてからすべてのJobの作業が完了するまでの期間において、各Jobの作業待ち時間の合計値が最小になるディスパッチングルールを、下記の解答群から選べ。 |
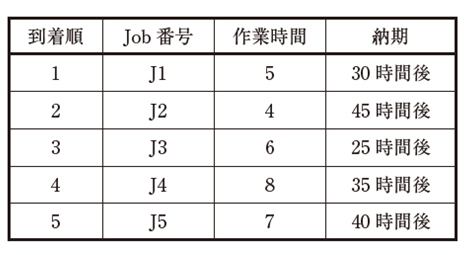 |
| ×ア 作業時間が長い順に作業する。 ○イ 作業時間が短い順に作業する。 ×ウ 到着が遅い順に作業する。 ×エ 到着が早い順に作業する。 ×オ 納期が早い順に作業する。 |
フローショップ
フローショップの問題は試行錯誤で時間がかかるので、最後に解きます。
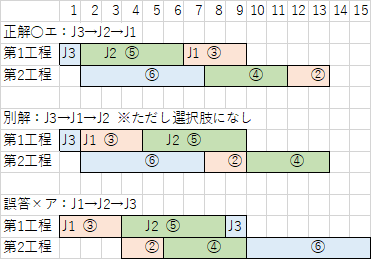
| 2 工程のフローショップにおけるジョブの投入順序を考える。各ジョブ各工程の加工時間が下表のように与えられたとき、生産を開始して全てのジョブの加工を完了するまでの時間(メイクスパン)を最小にする順序として、最も適切なものを下記の解答群から選べ。 |
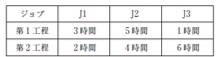
| ×ア J1 → J2 → J3 ×イ J1 → J3 → J2 ×ウ J2 → J1 → J3 ○エ J3 → J2 → J1 |
フローショップは総当たりで解くことが多く、時間がないときは鉛筆コロコロします。

| 製品A~Dの2 つの工程の加工時間が下表のように与えられたとき、2 工程のフローショップにおける製品の投入順序を検討する。 生産を開始して全ての製品の加工を完了するまでの時間(メイクスパン)を最小にする順序で投入した場合、メイクスパンに含まれる第1 工程と第2 工程の非稼働時間の合計値として、最も適切なものを下記の解答群から選べ。 |
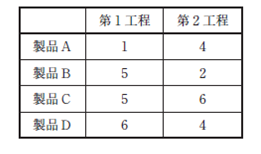 |
| ×ア 2 ×イ 3 ×ウ 4 〇エ 5 ×オ 6 |
個別生産でモノがあちこち行きかうのがジョブショップなら、決まった順にライン生産するのがフローショップです。「SPT順」はH30第4問で出ており、過去5年分を解いておけば正解できました。
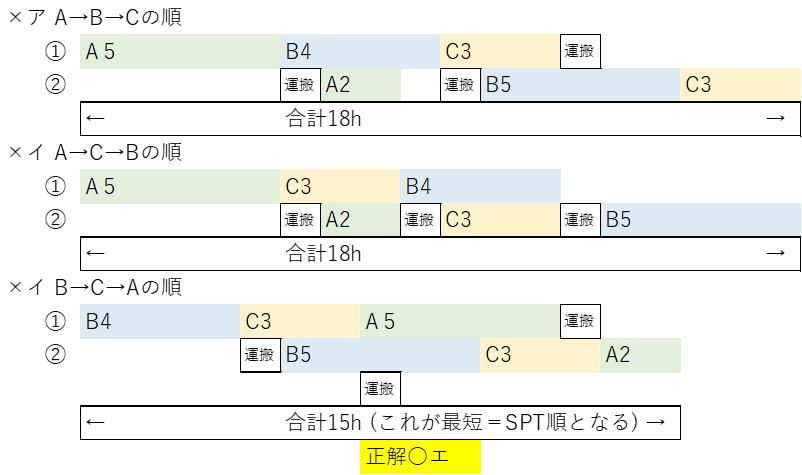
| ある職場に到着している3 種類の製品A、B、Cについて、生産を開始してからすべての製品の加工を完了するまでの時間(総所要時間)を最小化する生産順序について考える。この職場の作業条件は以下に示すとおりである。 |
| <作業条件> ・各製品は、最初に第1 工程で、次に、第2 工程で同じ順序で加工される。 ・各工程では一度加工が始まったら、その製品が完成するまで同じ製品を加工する。 ・工程間の運搬時間は1 時間とする。 ・各製品の各工程における加工時間は下表に示される。 |
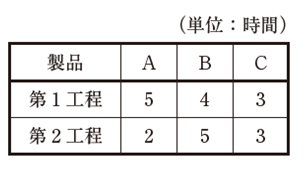 |
| 第1 工程における3 つの製品A、B、Cの投入順序に関する記述として、最も適切なものはどれか。 |
| ×ア A、B、Cの順に投入すると、総所要時間は17 時間である。 ×イ A、C、Bの順に投入すると、総所要時間は19 時間である。 ×ウ B、C、Aの順に投入すると、SPT 順に投入するよりも総所要時間は長くなる。 ○エ SPT 順に投入すると、総所要時間は15 時間である。 |
PERT
PERTとは、クリティカルパス=最も時間のかかる経路を見つけ、そこに手を入れてプロジェクト全体を時短する手法です。生産というより、ホワイトカラーのプロジェクトマネジメントに使います。
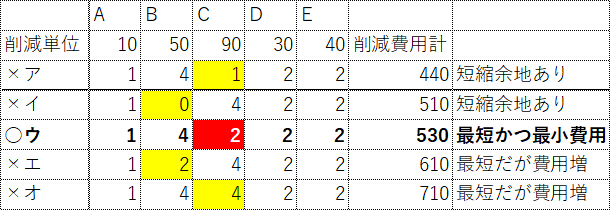
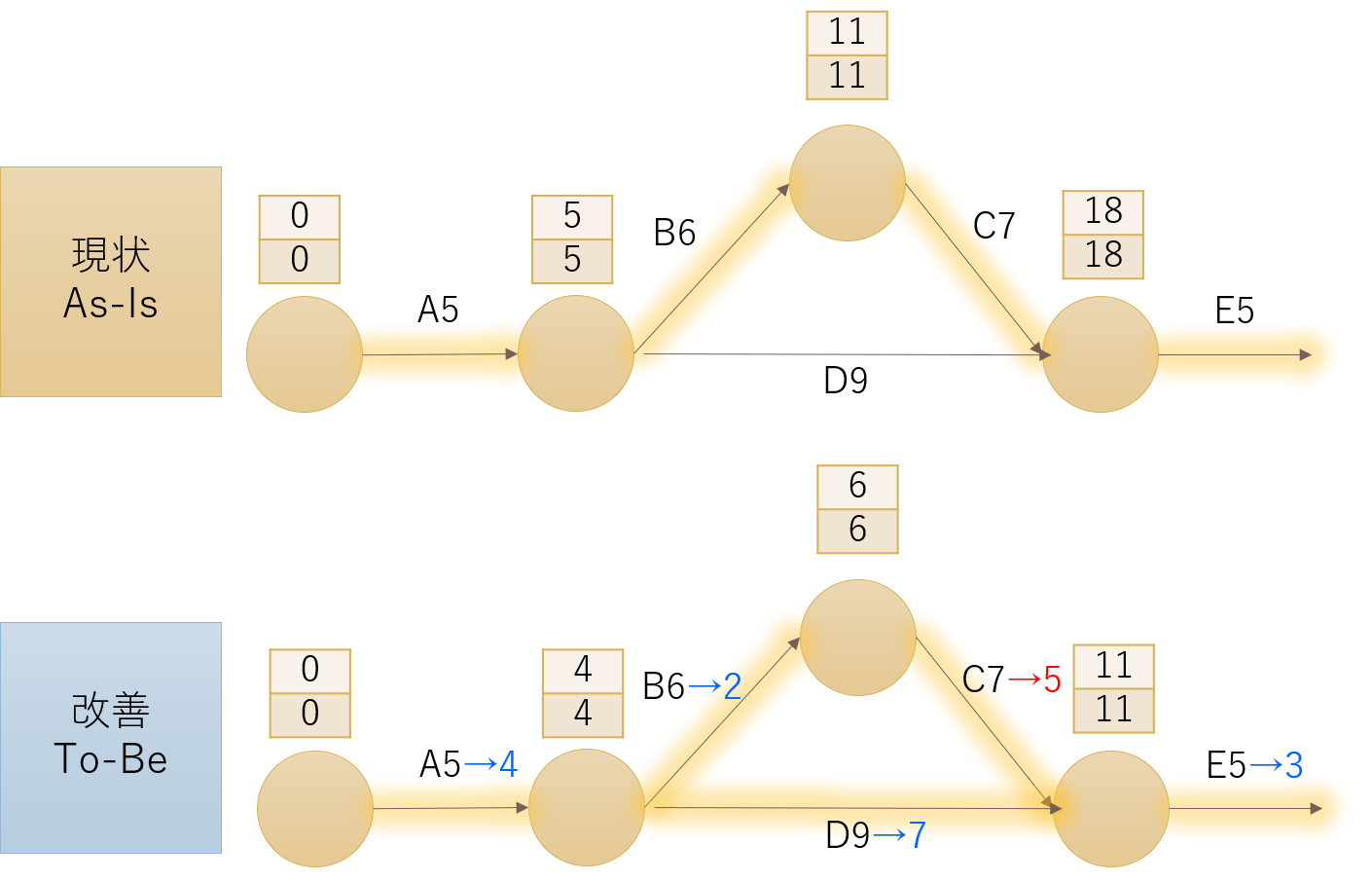
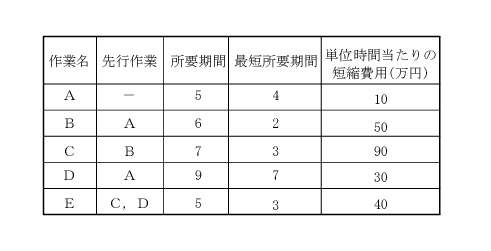
| 下表は、あるプロジェクト業務を行う際の各作業の要件を示している。CPM(Critical Path Method)を適用して、最短プロジェクト遂行期間となる条件を達成したときの最小費用として、最も適切なものを下記の解答群から選べ(単位:万円)。 |
ジョブショップの設問を、PERTを使って解きます。
| あるジョブは7 つの作業工程A~Gで構成されている。各作業工程の作業時間と作業工程間の先行関係が下表に示されるとき、このジョブの最短完了時間の値として最も適切なものを下記の解答群から選べ。 |
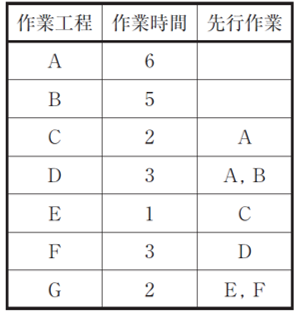 |
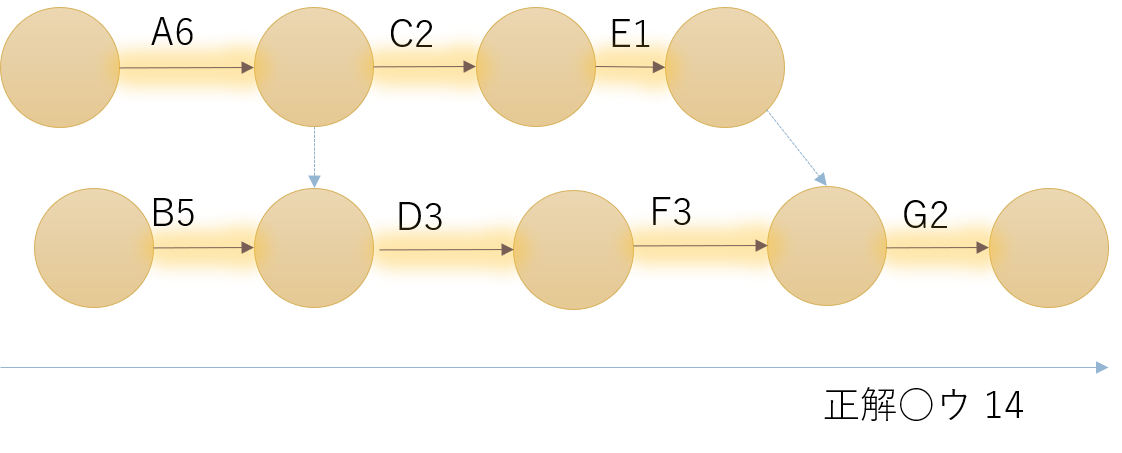
表からPERTを描くと、A→F→Gがクリティカルパスと分かるA,F,Gのうち費用最小のAを1h時短するので正解〇イ20万円に。PERTの作問としては易しい方です。

| 下表は、あるプロジェクト業務を構成する各作業の要件を示している。CPM(Critical Path Method)を適用して、現状のプロジェクト完了までの最短時間を明らかにした上で、その最短時間を1 時間短くするために必要な最小費用として、最も適切なものを下記の解答群から選べ(単位:万円)。 |
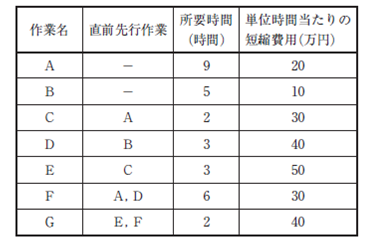 |
| ×ア 10 〇イ 20 ×ウ 30 ×エ 40 ×オ 50 |
PERTの図では以下の上段に「最速到達時間」、下段に「最遅着手時間」をメモすると見やすくなります。
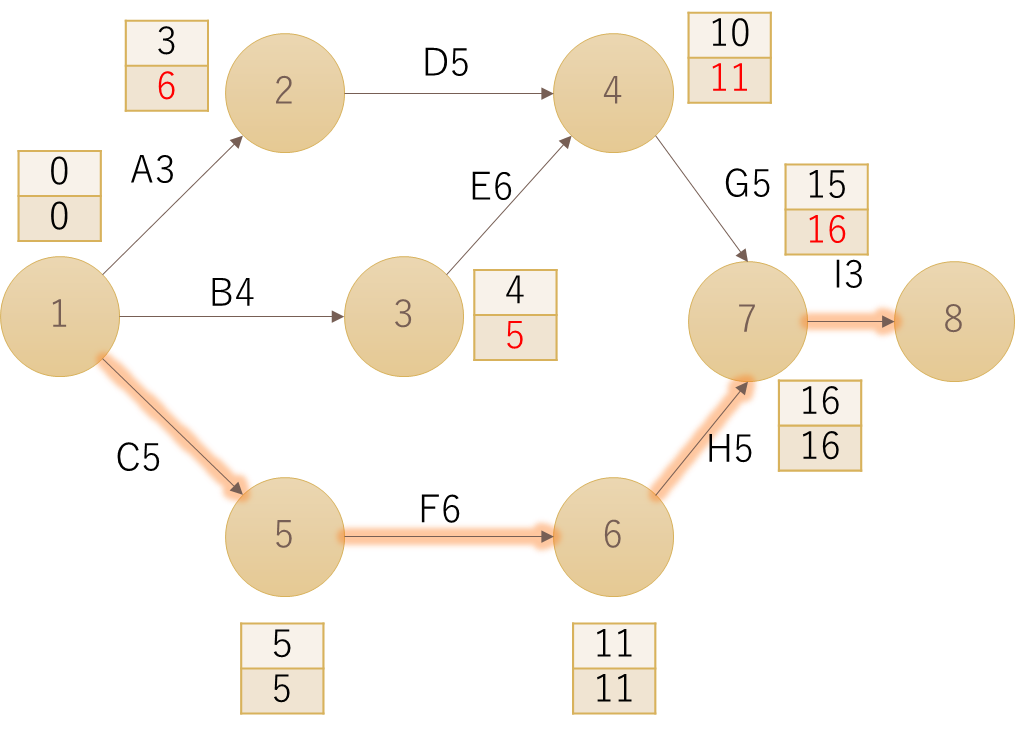
| × | →○ | |
| ×ア | 2 | 1 |
| ×イ | 2時間早くなる | 変わらない |
| ×ウ | 変わらない | 1時間早くなる |
| ×エ | 変わらない | 1→3→4→7になる |
| 以下は、あるプロジェクトにおけるPERT図であり、各作業の作業所要時間の予定が記載されている。この図のプロジェクトに関する記述として、最も適切なものを下記の解答群から選べ。 |
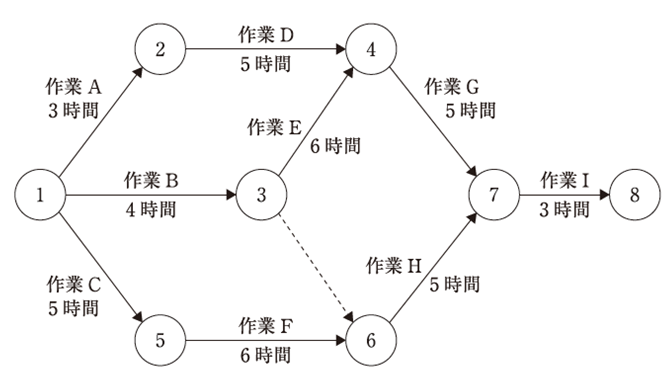 |
| ×ア 作業Cの終了時刻が2 時間早くなった場合、プロジェクトの完了時刻が2時間早くなる。 ×イ 作業Eの開始時刻が2 時間早くなった場合、プロジェクトの完了時刻が2時間早くなる。 ×ウ 作業Fの作業所要時間が1 時間短くなった場合、プロジェクトの完了時刻は変わらない。 ×エ 作業Fの作業所要時間が2 時間短くなった場合、クリティカルパスは変わらない。 ○オ 作業Hの作業所要時間が2 時間長くなった場合、クリティカルパスは変わらない。 |
線形計画法
当問はR4Ⅳ第2問(2)で問われた線形計画法(2条件セールスミックス)ですが、更に一ひねりした難問です。解き方として、複雑すぎる×エを後回しにしてアイウの改善(破線青・赤・緑)をするとマルA・B・Cの組み合わせでx、yを作ることができ、一番儲かるのがB→○イです。
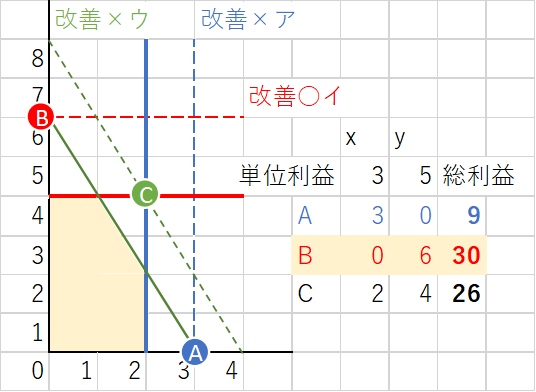
| ある工場では、3 台の機械を用いて2 種類の製品X、Yの生産が可能である。下表には、製品を1 単位生産するのに必要な各機械の工数と製品を1 単位生産して得られる単位利益、および現状で使用可能な各機械の工数が示されている。また、下図は、下表に示した各機械における使用可能工数の制約を図示したものである。 総利益が最も高くなる方策として、最も適切なものを下記の解答群から選べ。 |
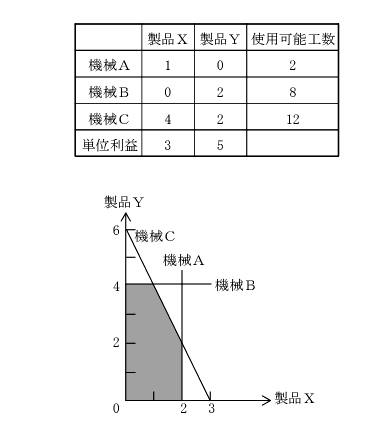
| ×ア 機械Aの使用可能工数を現状から4 引き上げて6 とする。 ○イ 機械Bの使用可能工数を現状から4 引き上げて12 とする。 ×ウ 機械Cの使用可能工数を現状から4 引き上げて16 とする。 ×エ 機械Bの使用可能工数を現状から2 引き上げて10、機械Cの使用可能工数を現状から2 引き上げて14 とする。 |
以前から事例Ⅳで「出る」「出る」とされた線形計画法(LP)が、ついにR4第2問で出題されました。するとおベテがムキになって暗記するので、それをからかうように当面出ません。
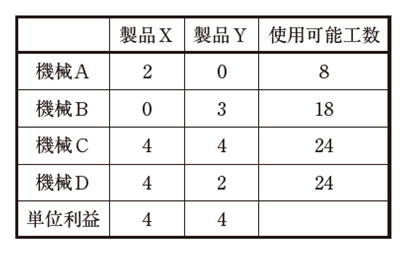
| ある工場では、4 台の機械設備を用いて2 種類の製品X、Yを生産することができる。下表には、製品を1 単位生産するのに必要な各機械の工数と製品を1 単位生産して得られる単位利益、および現状で使用可能な各機械の工数が示されている。また、参考として、下表に示した各機械における使用可能工数の制約を次ページに図示している。 総利益を最も高くする方策として、最も適切なものを下記の解答群から選べ。 |
 |
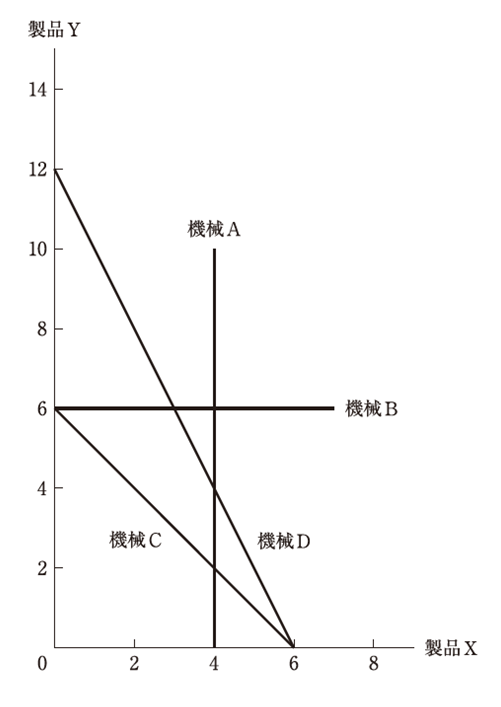 |
| ×ア 機械Aの使用可能工数を現状から4 引き上げて12 とする。 ×イ 機械Bの使用可能工数を現状から3 引き上げて21 とする。 ○ウ 機械Cの使用可能工数を現状から4 引き上げて28 とする。 ×エ 機械Dの使用可能工数を現状から4 引き上げて28 とする。 |
調達計画
調達計画の計算問題は、部品表と経済的発注量の2つ。いずれも易問なので確実に当てます。
部品表
「1次」部品表は、筆算で解ける簡単計算。そこでR1第7問(Aランク)⇔H28第9問(Dランク)の違いを調べます。
| 親1個あたり | × | →○ | |
| ×ア 部品c | 12 | 12 | 24 |
| ×イ 部品d | 48 | 36 | 96 |
| ○ウ 部品e | 32 | 64 | |
| ×エ 部品f | 8 | 60 | 16 |
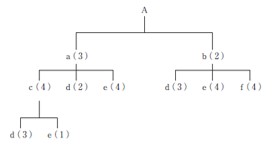
| 上図は、最終製品Aの部品構成表であり、( )内は親1 個に対して必要な部品の個数である。製品Aを2 個生産するとき、必要部品数量に関する記述として、最も適切なものを上記の解答群から選べ。 |
たまに難問やひっかけがある部品表としては、簡単な計算問題です。
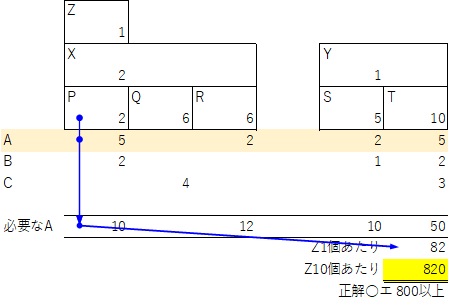
| 最終製品Zの部品構成表が下図に与えられている。( )内の数は親1 個に対して必要な子部品の個数を示している。製品Zを10 個生産するのに必要な部品Aの数量の範囲として、最も適切なものを下記の解答群から選べ。 |
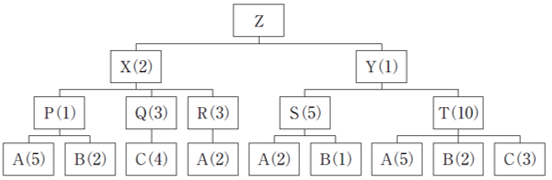 |
| ×ア 100 未満 ×イ 100 以上200 未満 ×ウ 200 以上800 未満 ○エ 800 以上 |
こちらは文章題ですが、部品表の役に立つのでここに載せます。×アウは独立⇔従属需要があべこべなので上図参照。×エはJIS定義そのままですが、暗記不要です。
| × | →〇 | |
| ×ア | 従属需要品目 | 独立需要品目 |
| ×イ | タイムバケット | 調達リードタイム |
| ×ウ | 独立需要品目 | 従属需要品目 |
| ×エ | 購買部門が調達する資材と部品 | 各部品を生産するのに必要な子部品の種類と数量 |
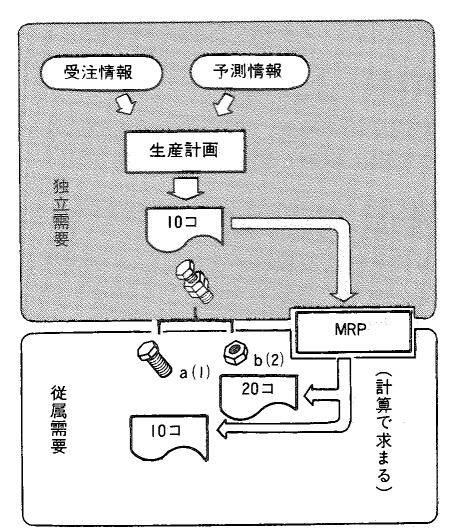
| 資材所要量計画に関する記述として、最も適切なものはどれか。 |
| ×ア 独立需要品目とは、資材調達先企業からの要望に従い、生産する時期と数量が決定される品目のことである。 ×イ 調達リードタイムとは、外部企業からの資材の調達にかかる所要時間のことである。 ×ウ 従属需要品目とは、営業部門とは無関係に、生産部門や資材調達部門が独自の需要予測に基づいて、生産する時期と必要量を決定する品目のことである。 ×エ 部品構成表とは、各部品を生産するのに必要な子部品の種類と数量をリスト化した表のことである。 〇オ 部品展開とは、計画期間内に生産する最終製品の種類と数量が決まったとき、それらを生産するのに必要な構成部品の種類とその数量を求めることである。 |
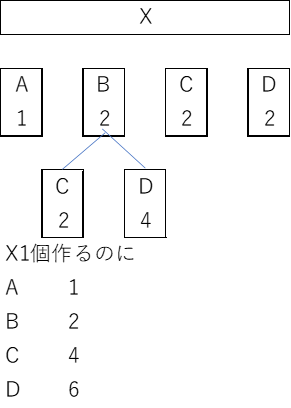
部品表としても簡単なパターンの問題。これも正解を選ぶのでなく、誤答全てのバツを正しく計算しなおして確実に当てます。
| × | →○ | |
| ×ア | 10 | 20 |
| ×ウ | 40 | 60 |
| ×エ | 40 | 20 |
| ×オ | 60 | 40 |
| 以下のストラクチャ型部品表に基づいた記述として、最も適切なものを下記の解答群から選べ。 |
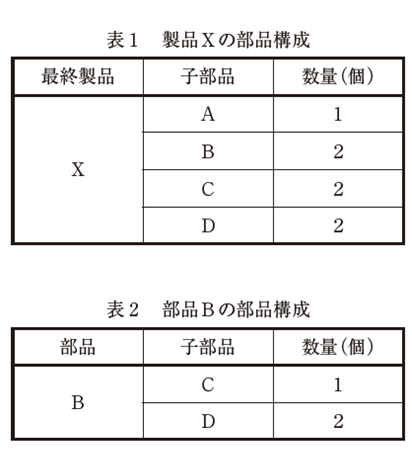 |
| ×ア 製品Xを10個生産するために、部品Bは10個必要である。 ○イ 製品Xを10個生産するために、部品Cは40個必要である。 ×ウ 製品Xを10個生産するために、部品Dは40個必要である。 ×エ 部品Bを20個生産するために、部品Cは40個必要である。 ×オ 部品Bを20個生産するために、部品Dは60個必要である。 |
発注計画、経済的発注量
トレードオフ(二律背反)な最小費用を計算させる経済的発注量(EOQ)は、イケカコ馬鹿が泣いて喜ぶH25「Ⅳ」(悪問)で応用出題済。「生産」ではその変形がちょくちょく出ます。
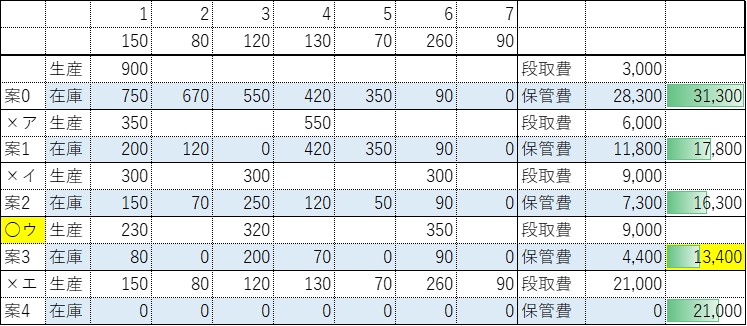
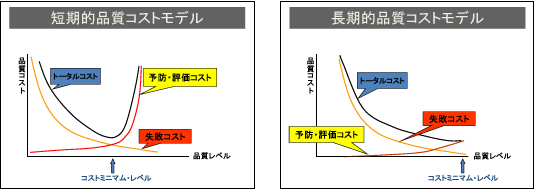
| 下表に示す7 日間の需要量(個)に対する生産計画を考える。製品を生産する日には、生産に先立ち段取りが必要で、1 回当たり段取り費3,000 円が発生する。また、生産した製品は当日以降の需要に充当することが可能であり、当日の場合は在庫保管費は発生しないが、翌日以降に繰り越す場合は、繰越在庫量に比例して、1 個1 日当たり10 円の在庫保管費が発生する。 生産計画の案0 は1 日目に7 日間の総需要量900 個を生産する計画で、総費用(段取り費と在庫保管費の合計)は31,300 円になる。 案1 ~ 4 は総需要量900 個を複数回に分けて生産する計画である。これらの中で総費用を最小にする案として、最も適切なものを下記の解答群から選べ。 |
経済的発注量(EOQ)は通常計算問題ですが、理論として文章題でも出せます。正答率Cになっていますが、どう見ても〇ウ一択の実質Aです。
| × | →〇 | |
| ×ア | 増える | 減る |
| ×イ | 減る | 増える |
| ×エ | 高く | 等しく |
| 経済的発注量に関する記述として、最も適切なものはどれか。 |
| ×ア 1 個1 期当たりの在庫保管費が増え、1 回当たりの発注費が減少した場合、経済的発注量は増える。 ×イ 1 個1 期当たりの在庫保管費が変化せず、1 回当たりの発注費が増えた場合、経済的発注量は減る。 〇ウ 経済的発注量で発注する場合、在庫保管費用と発注費用が等しくなる。 ×エ 経済的発注量で発注する場合、在庫保管費用より発注費用が高くなる。 |
経済的発注量に関する、超基本の論理問題。両辺を等号でつないてQを求めると、Q=√(2bd÷a)ですが、これを暗記するとベテになります。
| 経済的発注量モデルにおけるT期間の総費用を表す数式として、最も適切なものはどれか。 ただし、Q を1 回当たりの発注量、d を1 期当たりの推定需要量、a を1 回当たりの発注費、b を1 個1 期当たりの保管費とする。 |
| ×ア aTd/Q + bTQ ○イ aTd/Q + bTQ/2 ×ウ aTQ/2 + bTd/Q ×エ aTQ + bTd/Q |
設問文の条件を読み取らせる問題。ただし全パターンを計算すると時間ロスするので、【およそこの辺だろう】と割り切る力が必要です。
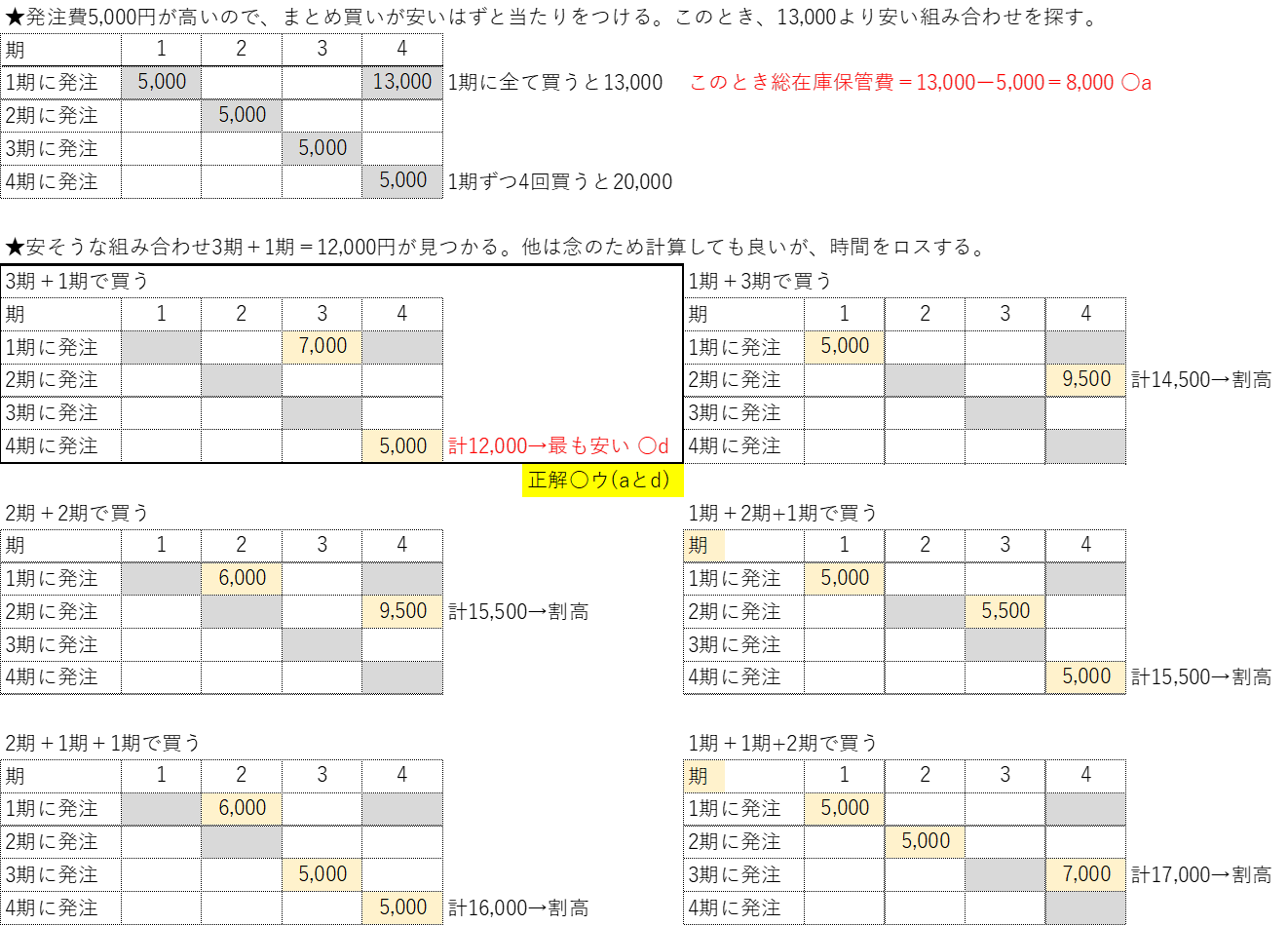
| ある製品についての最適発注計画を考える。製品の発注費は1 回当たり5,000円、保管費は1 個1 期当たり50 円である。ただし、製品は、期首に発注し即時に納入され、保管費は、翌期以降に持ち越された量にだけ発生するものとする。 下表は、毎期の予測需要量および最適発注計画を算出するための計算シートを示している。 例えば、「2 期に発注」の行と4 期の列で示されるセルの値9,500 は、2 期に2 期から4 期までの予測需要量の合計値70 を発注した場合の費用を示している。すなわち、3 期の予測需要量分10 が1 期間、4 期の予測需要量分40 が2 期間持ち越されることから、この発注に対する保管費が(10 × 1 + 40 × 2 )× 50 = 4,500 となり、これに発注費5,000 を加えた値が9,500 である。 |
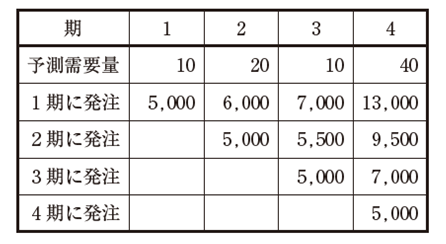 |
| この表から読み取れる記述の正誤の組み合わせとして、最も適切なものを下記の解答群から選べ。 |
| ○a 1 期に全期間の予測需要量を発注したときの総在庫保管費は、8,000 円である。 ×b 3 期の予測需要量が10 から15 に変更されると、最適発注計画の発注期は変化する。 ×c 最適発注計画では、1 期と3 期に発注が行われる。 ○d 最適発注計画の総費用は12,000 円である。 |
| a | b | c | d | |
| ×ア | 正 | 正 | 誤 | 誤 |
| ×イ | 正 | 誤 | 正 | 誤 |
| ○ウ | 正 | 誤 | 誤 | 正 |
| ×ウ | 誤 | 正 | 誤 | 正 |
| ×エ | 誤 | 誤 | 正 | 正 |
工数計画(IE)
苦手意識を持ちやすいIEですが、計算出題は実質時間研究(標準時間)だけ。ここは時間をかけてまとめて解いて、得意化します。
解説を理解するより、エクセルに入れて計算させる。すると楽して覚えます。
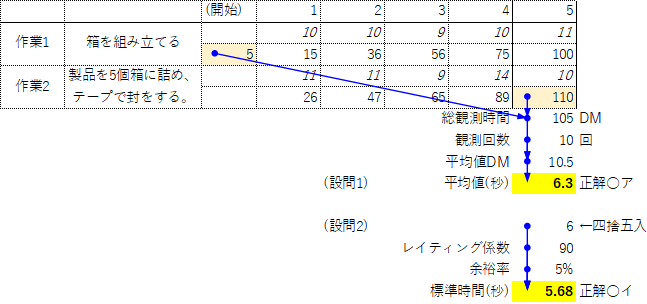
| ある工程では1 人の作業者が製品の箱詰めを行っている。この工程の標準時間を算出するため、作業内容を以下のように作業1 と作業2 に分割して、時間観測を行うこととした。 |
| 作業1 箱を組み立てる。 作業2 製品を5 個箱に詰め、テープで封をする。 |
| 作業者が「作業1 →作業2 」のサイクルを5 回繰り返したときの各作業の終了時刻を、ストップウオッチ(単位DM、ただし1 分=100 DM)を使って観測した。その結果を観測用紙に記入したものが下表である。ただし、観測開始時点のストップウオッチの目盛りは5 DM であった。 作業1 に関する下記の設問に答えよ。 |
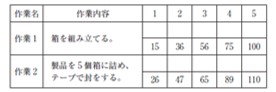
| (設問1 ) 観測時間の平均値(単位:秒)として、最も適切なものはどれか。ただし、観測時間の平均は算術平均を用いる。 |
| ○ア 6 ×イ 10 ×ウ 11 ×エ 56 |
| (設問2 ) レイティング係数が90 と観測され、余裕率を5 %と設定したときの標準時間(単位:秒)として、最も適切なものはどれか。 |
| ×ア 5.1 ○イ 5.7 ×ウ 6.4 ×エ 7.1 |
当問は正解○エだけ先に図解。R1第5問ジョブショップスケジューリングと論点またぎの類題になっていて、サイクルタイム最小=生産量最大に。
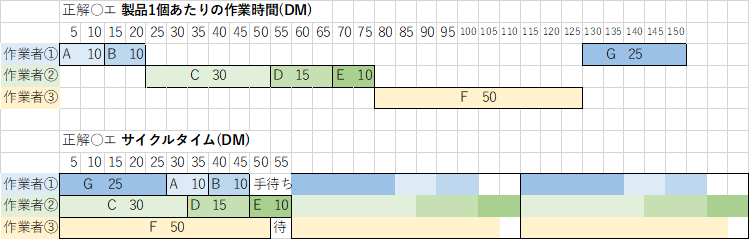
| ある製品の梱包工程の作業内容は下表に示すとおりである。 この工程を3 名の作業者で分担して作業を行う案として、単位時間当たりの生産量が最も多いものを下記の解答群から選べ。 ただし、各作業者間の移動・搬送の時間は無視でき、スペースの制約は考えない。 |
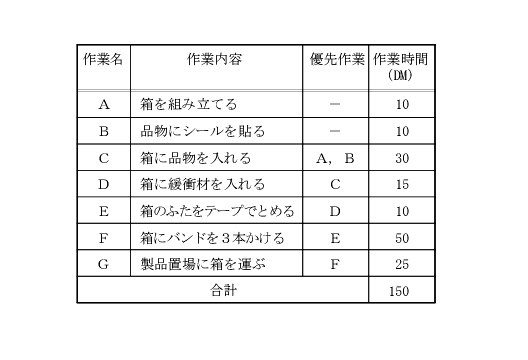
| ×ア 作業者①がA・B・C・D、作業者②がE・F、作業者③がGを担当する。 ×イ 作業者①がA・B・C・Dを担当し、作業者②がEを実施したのち、作業者②と③が組作業によってFを実施(作業時間が25 DM になる)したのち、作業者③がGを担当する。 ×ウ 作業者①がB・C・D、作業者②がE・F、作業者③がA・Gを担当する。ただし、あらかじめいくつかの箱を組み立てておく。 〇エ 作業者①がC・D・E、作業者②がF、作業者③がA・B・Gを担当する。ただし、あらかじめいくつかの箱を組み立てて、品物にシールを貼っておく。 |
解説は後日作成します。
| あるプレス工程では、1 人の作業者が以下のような手順①、②で作業を行っている。 |
 |
| この手順①、②を1 サイクルとして、ストップウオッチを使って時間研究を実施した結果、1 サイクルの正味作業の観測時間の平均値は90 秒、レイティング係数は110 であった。次に、この作業者についてワークサンプリングを実施し、延べ500 回の計測の中で余裕に該当するサンプルの数が60 観測された。 この結果を用いて標準時間を求めたとき、この1 サイクルの標準時間として、最も適切なものはどれか。 |
| ×ア 90 秒未満 ×イ 90 秒以上95 秒未満 ×ウ 95 秒以上100 秒未満 〇エ 100 秒以上 |
難問になりやすいIE時間研究論点にしては、内掛け・外掛けの違いがわかれば当たるサービス問題です。当サイトではこの手の計算問題は自力でエクセル化を提唱しています。
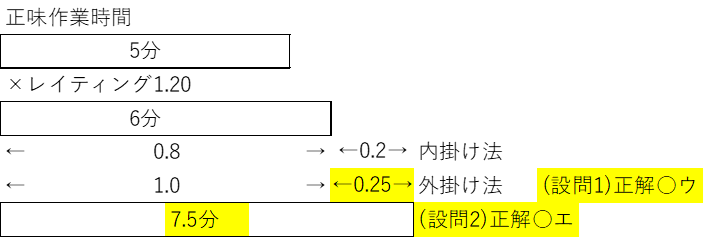
| 金属部品を人手で加工する作業の標準時間を計算するためのデータとして、 正味作業の観測時間:5分/個 レイティング係数:120 内掛け法による余裕率:0.20 の値を得た。 このとき、下記の設問に答えよ。 |
| (設問1 ) この作業に対する外掛け法による余裕率の値として、最も近いものはどれか。 |
| ×ア 0.15 ×イ 0.20 ○ウ 0.25 ×エ 0.30 ×オ 0.35 |
| (設問2 ) この作業の標準時間として、最も近いものはどれか(単位:分/個)。 |
| ×ア 6.25 ×イ 6.50 ×ウ 7.00 ○エ 7.50 ×オ 7.75 |
品質Q・設備M
検定は割り切って捨てる。設備総合効率⇔設備投資のどちらかが出る設備は1マーク当てに行く。設備総合効率は良問R4第18問をエクセルにして理解完了です。
検定
検定なんて、どのテキストにも載っていない。解けるワケがありません。
| ある工場では、製品Aの加工精度のバラツキを抑制する目的で新設備を導入した。バラツキが抑制できたかどうかを仮説検定により確認するために、新設備を用いて生産した製品10 個の加工精度を測定した。 このときに行う仮説検定の手順に関する記述として、最も適切なものはどれか。 ただし、従来の設備では、加工精度の分散が23.5 であった。 |
| ×ア 10 個のデータの分散が23.5 よりも小さいかどうかを調べる。 ×イ 検定統計量がF 分布に従うことを利用して検定を行う。 ×ウ 検定統計量は10 個のデータから計算される偏差平方和である。 ×エ 対立仮説、有意水準、データ数に基づいて、帰無仮説の棄却域を設定する。 〇オ 対立仮説をθ2 =23.5 と設定する。 |
| 以下の文章を読んで、下記の設問に答えよ。 |
| ある工作機械において、現行の加工条件よりさらに良い条件を探すため、2 水準系のL 8 直交配列表を用いた実験を計画することとなった。調べたい因子および交互作用は、以下のとおりである。 |
| 因 子:A、B、C、D 交互作用:A×B、A×C |
検定は解説しません。
| A | B | |
| ×ア | 1.833 以上となった | いえる |
| ×イ | 1.833 より小さくなった | いえない |
| ×ウ | 1.860 以上となった | いえる |
| ○エ | 1.860 より小さくなった | いえない |
| ×オ | 1.860 より小さくなった | いえる |
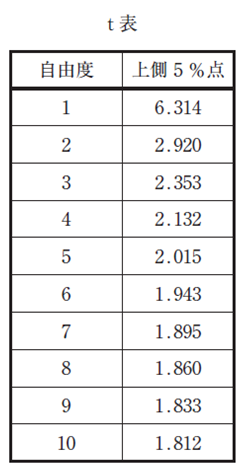
| 統計的検定に関する以下の文章の空欄AとBに入る語句の組み合わせとして、最も適切なものを下記の解答群から選べ。なお、検定においては、下のt 表を使用すること。 |
| ある製品特性の平均値は65.5 である。この特性について、技術部門で新しい生産条件を設定して実験し、9 個のサンプルを得た。その平均値は71.0、標準偏差は9.0 であった。生産条件の変更によって特性の平均値が上がったか否かを、有意水準5 %でt 検定したところ、検定統計量の値は【A】 。これより、生産条件の変更によって平均値は上がったと【B】。 |
 |
設備効率
「情報」で教わるMTBF、MTTRの設問ですが、ここでは設備総合効率「性能稼働率」の知識として使います。
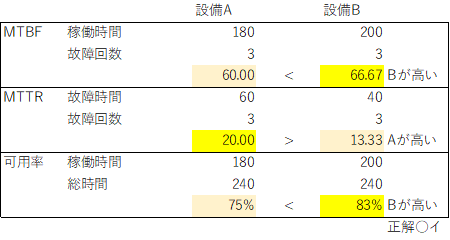
| 初期導入された設備AとBを240 時間利用したときの稼働および故障修復について、下図のような調査結果が得られた。この2 台の設備に関する記述a~cの正誤の組み合わせとして、最も適切なものを下記の解答群から選べ。 |
 |
| ○a MTBF(平均故障間隔)は設備Bのほうが長い。 ×b MTTR(平均修復時間)は設備Bのほうが長い。 ○c アベイラビリティ(可用率)は設備Bのほうが高い。 |
| a | b | c | |
| ×ア | 正 | 正 | 誤 |
| ○イ | 正 | 誤 | 正 |
| ×ウ | 正 | 誤 | 誤 |
| ×エ | 誤 | 正 | 正 |
| ×オ | 誤 | 正 | 誤 |
与えられた式に代入すると1.67になるので、アイの2択に。後は指数の大小どちらが良いかで決めます。

| ある工程が規格に対して満足な状態かどうかを管理するために、この工程で生産される製品の品質特性の発生頻度を測定した。その結果、平均2.05、標準偏差0.05であった。この品質特性については、規格の中心が2.05、規格下限値が1.8、規格上限値が2.3 と決められている。この調査結果から分かることに関する記述として、最も適切なものを下記の解答群から選べ。 |
| ここで、工程能力指数は以下の式で求められるものとする。 工程能力指数= 規格の幅/(6 ×標準偏差) また、工程能力の評価基準として1.33 を用いるものとする。 |
| ×ア この工程の工程能力指数は1.33 を上回っているので規格値からはみ出す製品があり、十分な工程能力があるとはいえず、改善が必要である。 ○イ この工程の工程能力指数は1.33 を上回っているので十分な工程能力があり、工程は満足な状態で管理されている。 ×ウ この工程の工程能力指数は1.33 を下回っているので規格値からはみ出す製品があり、十分な工程能力があるとはいえず、改善が必要である。 ×エ この工程の工程能力指数は1.33 を下回っているので十分な工程能力があり、工程は満足な状態で管理されている。 |
問題集の解説を読むより、自分でエクセルにして数値を決める。すると一回で基本を覚え、「Ⅳ」の難問を解く力も同時に上がります。
| 最も高い | その次 | 3番目 | |
| ×ア | a | b | c |
| ×イ | b | a | c |
| 〇ウ | b | c | a |
| ×エ | c | a | b |
| ×オ | c | b | a |
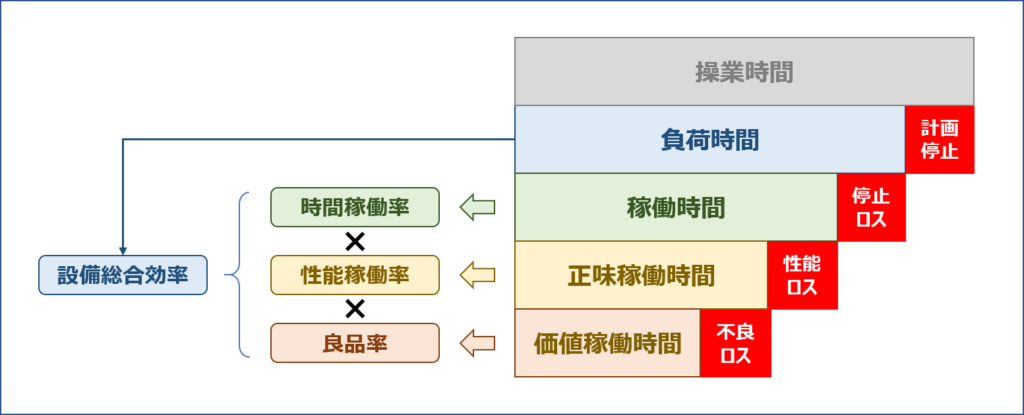
設備総合効率(当問)の押さえ方
①時間稼働率→性能稼働率→良品率の順にエクセルで計算する(現行が45%)
②施策abcの結果がどうなるか、それぞれエクセルで計算
③すると改善後の設備総合効率がb→c→aの順と分かる

当然ですが、本試験中の筆算でこんな問題を解ける筈がなく、試験後の復習で理解させる出題。過去問集のヘタクソ解説を避け、エクセルを自作すれば一発で理解できる良問です。
| ある設備について、1,000 時間の負荷時間内での設備データを収集したところ下表が得られた。 |
 |
| 以下の改善施策を、期待される設備総合効率の高い順に並べたものとして、最も適切なものを下記の解答群から選べ。ただし、負荷時間は同じで、その他の条件も変わらないものとする。 |
| a 不適合の原因を検討して、不適合品率を20 %から15 %にする。 b 速度低下の原因を改善して、加工数量を6,720 個から7,680 個にする。 c 段取作業を改善して、停止時間を半減させ、稼働時間を800 時間から900 時間にする。 |
資本回収係数→年金現価係数と読み替えれば、「事例Ⅳ」の問題に。×年金終価係数は誤答ダミーです。
| ある工程を自動化するためには、設備の改良に1,000 万円を投資する必要がある。この自動化投資を6 年で回収するために必要な最小の原価低減額(万円/年)として、最も適切なものを下記の解答群から選べ。計算利率を8 %とし、必要ならば下表の換算係数を使うこと。 |
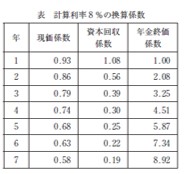
| ×ア 136 ×イ 167 ×ウ 190 ○エ 220 |
「追加投資案の割引回収期間」なる難論点なので、仮定として解説します(違っていれば訂正します)。①追加投資C-B、C-Aがいずれもプラスなので、Cを最大とする。 ②次にC-A、C-Bを比べるとAの方が回収に時間がかかるので、A>Bになる。するとNPVはC>A>Bになる。少々苦しいですが、これで解説に代えます。
| 設備自動化のための投資案A、B、Cの割引回収期間を計算したところ、表1 の結果が得られた。さらに、投資案を分析するために、投資案A、B、Cの中から任意の2 つ(例えば、案Aと案B)を選んで初期投資額の差と経費節減額の差をとった追加投資案の割引回収期間を計算したところ、表2 の結果が得られた。 各投資案の正味現在価値利益PA、PB、PCを大きい順に並べたときの順序として、最も適切なものを下記の解答群から選べ。投資の計画期間は10年間とする。 |
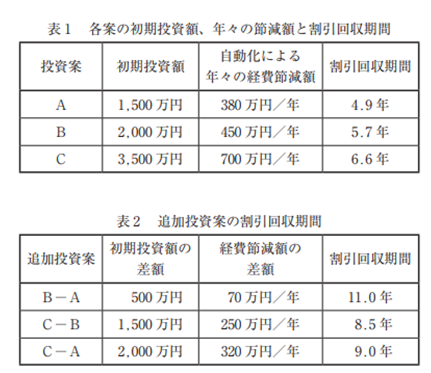 |
| ×ア PA > PB > PC ×イ PA > PC > PB ×ウ PB > PA > PC ○エ PC > PA > PB ×オ PC > PB > PA |
店舗管理17マーク
商圏分析
商圏分析は難しめの出題が続きますが、テキスト掲載論点でもあり、できれば当てたい1マークです。
当問は下図の結論を知っていれば簡単で、A⇔B市の人口が4倍なら、距離が2:1になる地点が商圏分岐です。なお失業率はダミー条件。

| A市とB市との2 つの市の商圏分岐点を求めたい。 下図で示す条件が与えられたとき、ライリー&コンバースの法則を用いて、B市から見た商圏分岐点との距離を求める場合、最も適切なものを下記の解答群から選べ。 |

| ×ア 2.5 km ×イ 3 km ○ウ 5 km ×エ 7.5 km ×オ 10 km |
A市は人口で4倍ですが、距離が2倍=1/4の吸引力になるので、差し引き1:1になります。
| A市とB市が、その中間にあるX町からどの程度の購買力を吸引するかを求めたい。下図の条件が与えられたとき、ライリーの法則を用いてA市とB市がX町から吸引する購買力の比率を求める場合、最も適切なものを下記の解答群から選べ。 |
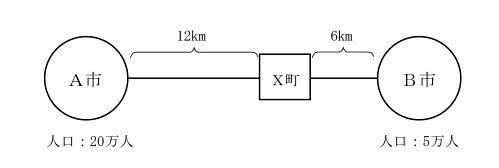 |
| 〇ア A市:B市= 1 : 1 ×イ A市:B市= 2 : 1 ×ウ A市:B市= 1 : 2 ×エ A市:B市= 8 : 1 ×オ A市:B市= 1 : 8 |
ライリー=コンバース(都市単位)を店舗単位にすると修正ハフモデル。経産省お墨付きなので、割り切って覚えます。

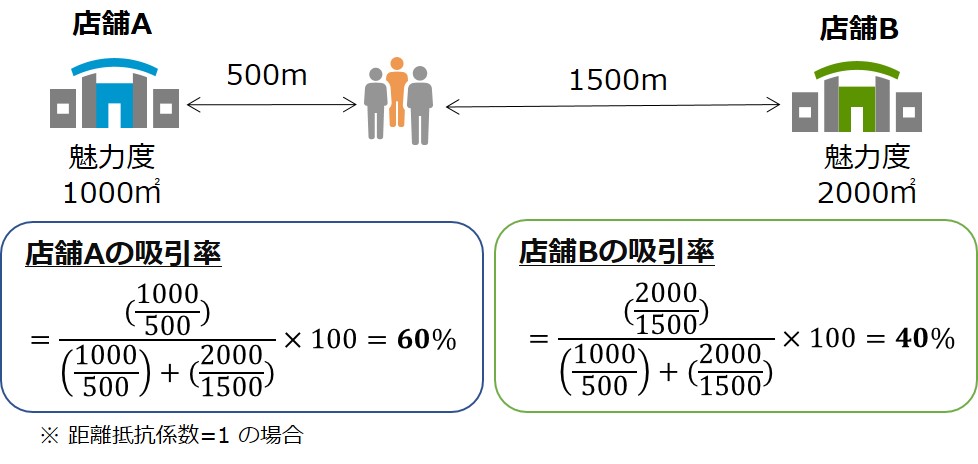
| ある地域に住む消費者Xが、ある店舗に買い物に出かける確率を考えたい。その地域には店舗Aおよび店舗Bの2 店舗のみが存在すると仮定する。このとき、消費者Xが店舗Aに買い物に出かける確率を計算したい。以下で示す条件が与えられたとき、修正ハフモデルを用いて上記の確率を求める場合、最も適切なものを下記の解答群から選べ。なお、店舗の魅力度については売場面積を使用する。 |
| 店舗Aの売場面積 :1,000 m2 店舗Aと消費者Xとの距離:1,000 m 店舗Bの売場面積 :2,000 m2 店舗Bと消費者Xとの距離:2,000 m 距離抵抗係数 :2 |
修正ハフモデルを単純に考えると、【面積比=距離の2乗の時に】その魅力が1:1に。当問を約分して考えると店舗Aの魅力=5/4、同Bの魅力=8/4を計算できるので、Bの吸引度=8/(5+8)で〇ウ。エクセルで自作してみましょう。
| ある地域に住む消費者Xが、ある店舗に買い物に出かける確率を考えたい。その地域には店舗Aと店舗Bの2 店舗のみが存在する。このとき、消費者Xが店舗Bに買い物に出かける確率を計算したい。以下で示す条件が与えられたとき、修正ハフモデルを用いて上記の確率を求める場合、最も適切なものを下記の解答群から選べ。なお、店舗の魅力度については売場面積を使用する。 |
| 店舗Aの売場面積 :1,500 m2 店舗Aと消費者Xとの距離:800 m 店舗Bの売場面積 :600 m2 店舗Bと消費者Xとの距離:400 m 距離抵抗係数 :2 |
| ×ア 5/13 ×イ 4/9 ○ウ 8/13 ×エ 8/9 |
MD・予算計画
この論点は以前はGMROIが頻出でしたが、最近は相乗積が出ます。テキストレベルなので両方押さえましょう。
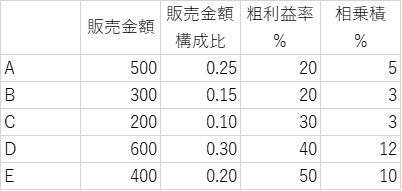
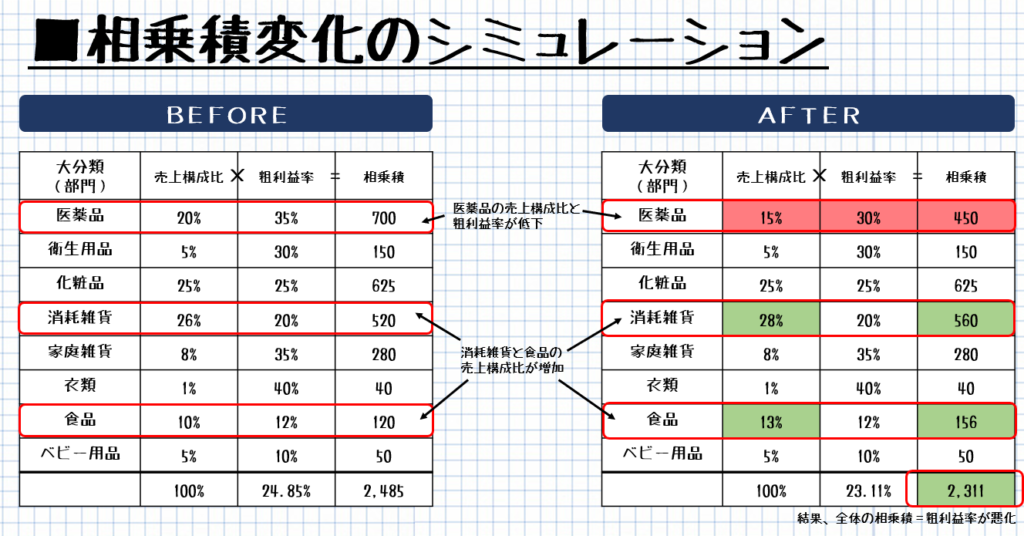
過去問解説を読む時間はムダ。以下を参考にエクセル自作を。
| × | →○ | |
| ×ア | 2倍 | 1倍 |
| ×イ | 50% | 5% |
| ×エ | 大きい | 同じ |
| ×オ | カテゴリーE | 〃D |
| 店舗Xのある月の営業実績は下表のとおりである。この表から計算される相乗積に関する記述として、最も適切なものを下記の解答群から選べ。 |
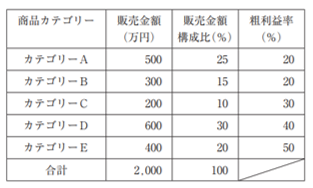
| ×ア カテゴリーA~Eの合計の販売金額が2 倍になると、各カテゴリーの相乗積の合計は1倍になる。 ×イ カテゴリーAの相乗積は5 % である。 ○ウ カテゴリーAの販売金額も粗利益率も変わらず、他のカテゴリーの販売金額が増加すると、カテゴリーAの相乗積は減少する。 ×エ カテゴリーBはカテゴリーCよりも相乗積が同じ。 ×オ 相乗積が最も大きいカテゴリーは、カテゴリーDである。 |
値入率には、売価・原価の2つあるので、ボックス図を描いて整理します。

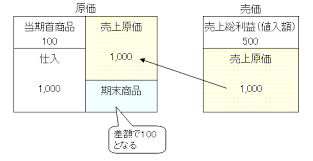
| 下表の5 種類の商品を仕入れて販売することを計画している。 商品A~Eの中で、同じ売価に設定される商品が2 つある。この2 つの商品について、仕入れた数量をすべて設定した売価で販売したときの粗利益額の合計として、最も適切なものを下記の解答群から選べ。なお、それぞれの商品の売価は、売価値入率により設定されるものとする。 |
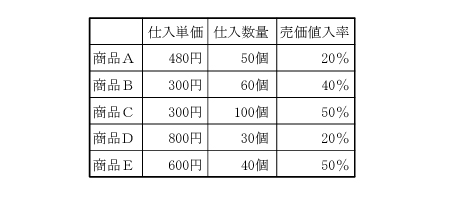
| ×ア 12,000 円 ○イ 36,000 円 ×ウ 42,000 円 ×エ 60,000 円 ×オ 90,000 円 |
相乗積=粗利益率×売上高比率で、相乗積を累計すると全社の粗利益率に。当問はその使い方を学ぶ良問です。
| 下表は、店舗Xにおける、ある期間の商品カテゴリー別の売上高と粗利益率、相乗積を示したものである。この表を見て、下記の設問に答えよ。なお、表内の(値1 )~(値3 )については、必要に応じて計算すること。 |
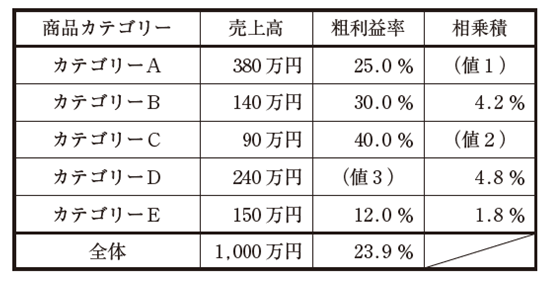 |
| (設問1 ) 店舗Xにおいて、表に示した販売期間の粗利益高が2 番目に小さい商品カテゴリーはどれか。 |
| ×ア カテゴリーA ×イ カテゴリーB ○ウ カテゴリーC ×エ カテゴリーD ×オ カテゴリーE |
| (設問2 ) 店舗Xにおける販売計画の考え方に関する記述として、最も適切なものはどれか。 ただし、商品カテゴリーごとの粗利益率は一定で、それぞれの商品カテゴリーの売上は他の商品カテゴリーの売上に影響しないものとする。 |
| ×ア カテゴリーAの取り扱いをやめると、全体の粗利益率は上昇する。 ○イ カテゴリーBの売上高が2 倍になると、全体の粗利益率は上昇する。 ×ウ カテゴリーCの売上高が2 倍になった場合は、カテゴリーBの売上高が2 倍になった場合よりも全体の粗利益高の増加額が大きい。 ×エ カテゴリーDの売上高が半分になると、全体の粗利益率は低下する。 ×オ カテゴリーEの売上高が10倍になると、全体の粗利益高は2 倍以上に増加する。 |
| × | →○ | |
| ×ア | 上昇 | 低下 |
| ×ウ | 大きい | 小さい |
| ×エ | 低下 | 上昇 |
| ×オ | 10 | 13.5 |
こちらは単純な分数問題です。
| 下表は、店舗Xにおける、ある期間の売場別の売上高、粗利益率、SKU 数、ゴンドラ本数を示したものである。 売場Aから売場Eの5 つの売場の生産性に関する記述として、最も適切なものを下記の解答群から選べ。 なお、ここでは、スペース生産性はゴンドラ1 本当たりの粗利益高で評価し、営業利益は粗利益から管理コストを差し引いたものとして計算する。管理コストは1SKU 当たり同一であるとする。また、表に記載した内容以外の条件については、すべて同一であることとする。 |
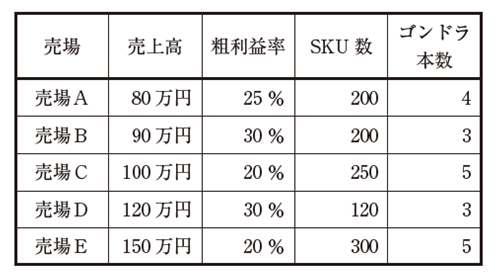 |
| ×ア 売場Aと売場Cの1 SKU 当たりの粗利益高は同じである。 ○イ ゴンドラ1 本当たりの営業利益額が最も高いのは売場Dである。 ×ウ 商品の自動発注システムを導入して1 SKU 当たりの管理コストが半分になったとすると、そのときの営業利益額の増加額が一番大きい売場は、売場Bである。 ×エ すべての売場でゴンドラ本数を1 本ずつ減らしたとき、売場ごとの売上高がそれぞれ3 割減少しても、すべての売場でスペース生産性が高まる。 ×オ 最もスペース生産性が高い売場は、売場Eである。 |
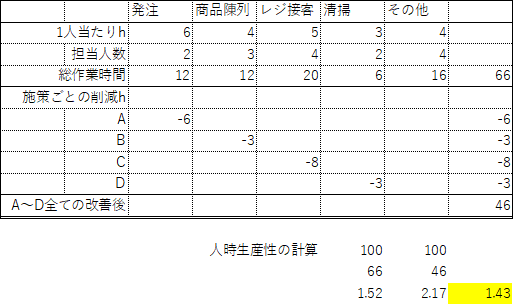
簿記と異なり計算手順の決まりはないので、時間をかけてエクセルにしてみる。↓の図では、作業時間⇔削減時間の絶対値で比較しました。
| × | →○ | |
| ×ア | 2倍以上 | 約1.4倍 |
| ×イ | 改善策AとB 改善策CとD | 改善策A(6) 改善策B(3)とD(3) |
| ×エ | 大きい | 小さい(BとD6<C8) |
| ×オ | 改善策A | 改善策C |
| 下表は、店舗Xにおける1 日の作業全体をまとめたものである。この表に基づく以下の【人時生産性の改善策】A~Dに関する記述として、最も適切なものを下記の解答群から選べ。ただし、改善策による売上高・粗利益額の変動はないものとして答えよ。 |
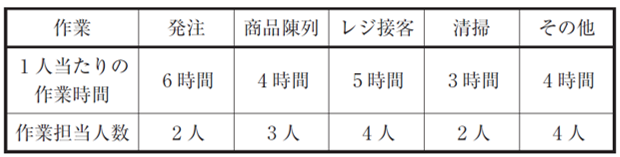 |
| 【人時生産性の改善策】 A 自動発注システムを導入し、発注の担当人数を 1 人減らす。 B 商品陳列に段ボール陳列やシェルフレディパッケージを導入して、 1 人当たりの作業時間を 25 %削減する。 C セルフレジを導入してレジ接客の担当人数を 1 人減らし、 1 人当たりの作業時間を 20 %削減する。 D 清掃ロボットを導入して清掃の 1 人当たりの作業時間を 50 %削減する。 |
| 〔解答群〕 ×ア AからDのすべての改善策を行うと、全体の人時生産性は 約1.4倍に高まる。 ×イ 改善策A(6)を同時に行う場合と、改善策B(3)とD(3)を同時に行う場合とで人時生産性の改善効果は同じである。 〇ウ 改善策Bと改善策Dの人時生産性の改善効果は同じである。 ×エ 改善策Bと改善策Dを同時に行う場合の人時生産性の改善効果は、改善策Cを単独で行うよりも小さい。 ×オ 人時生産性の改善効果が最も高いのは、改善策Cである。 |
物流
物流は当てやすいサービス論点ですが、時々変な計算問題が出ます。
エシュロン在庫といっても難しくなく、自社(工場)から見た川下にある全在庫量のことです。
| ある工場では、下図に示すように、 3 つの配送センターを経由して 6 つの店舗に製品を配送している。工場、配送センター、店舗の上の数値は、それぞれの拠点にある現時点の在庫量を示し、矢印の上の数値は現時点における配送中の製品量を示している。 配送センターBの現時点におけるエシェロン在庫量として、最も適切なものを下記の解答群から選べ。 |
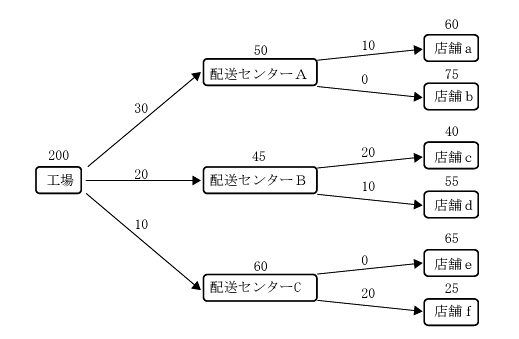 |
| ×ア 45 ×イ 75 〇ウ 170 ×エ 265 ×オ 390 |
| ① | ② | ③ | |
| ×ア | a | b | c |
| ×イ | a | c | b |
| ×ウ | b | c | a |
| ×エ | c | a | b |
| ○オ | c | b | a |
| トラック運送における共同輸配送に関する以下の【取組内容】と、取組前よりも改善が期待される【生産性指標】の組み合わせとして、最も適切なものを下記の解答群から選べ。 |
| 【取組内容】 | 【生産性指標】 |
| ① 取組前には、荷主Aと荷主Bそれぞれの貨物を異なるトラックに積んでも、両方のトラックに他の貨物を積載する余裕があったため、荷主Aと荷主Bの貨物を同じトラックに積み合せることにした。 | c 積載率(貨物積載して走行するトラックの最大積載量に占める、実際に積載した貨物の量の割合) |
| ② 取組前には、荷主Cの貨物を着地でトラックから降ろした後に帰り荷がなかったため、荷主Cの納品後に荷主Dの貨物を帰り荷として積載することにした。 | b 実車率(トラックの走行距離に占める、実際に貨物を積載して走行した距離の割合) |
| ③ 取組前には、荷主Eの貨物を積載したトラックが、発地X・着地Y間を宿泊を伴いながら往復運行し、荷主Fの貨物を積載したトラックが、発地Y・着地X間を宿泊を伴いながら往復運行していた。このため、両方のトラックが発着地X・Y間の中間地点で出会い、互いの貨物を積み替えて宿泊を伴わずに輸送することにした。ただし、トラック1 台に乗車するドライバーは1 人とする。 | a 実働率(トラックの運行可能な時間に占める、走行や荷役、手待ちなど実際に稼働した時間の割合) |
| トラックの積載率を改善させるために、取組案aとbを検討している。 現状では、物流センターAと物流センターBからそれぞれ別々にトラック1 台が走行し、物流センターCへ納品しており、各物流センターから輸送する際の実車の積載率は50 %未満である。(下図参照) |
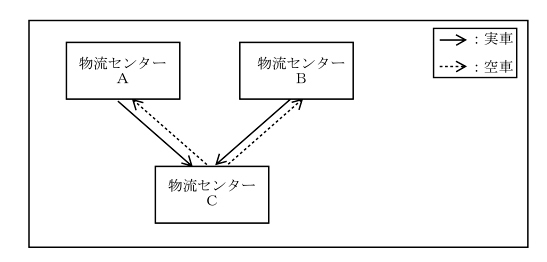 |
| 取組案aとbは、それぞれ以下のとおりである。 取組案a 物流センターAの納品分を物流センターBに集めた後、物流センターBからま とめて物流センターCへ別のトラック1 台で納品する。(下図参照) |
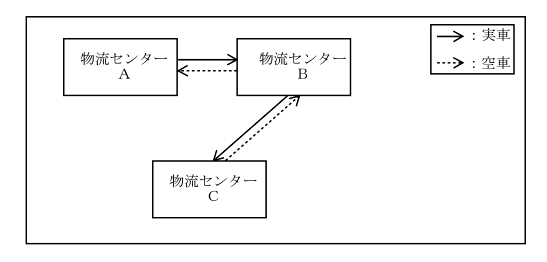 |
| 取組案b 物流センターCから物流センターAと物流センターBをトラック1 台が巡回し て集荷し、物流センターCへ納品する。(下図参照) |
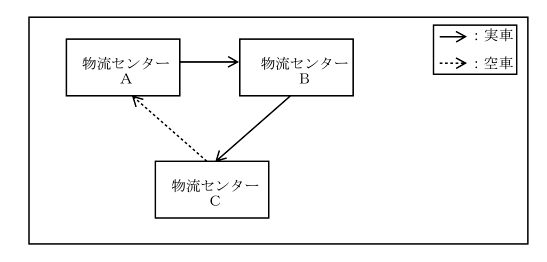 |
| 上記の取組案aとbに関する記述として、最も適切なものはどれか。 ただし、ここでいう積載率とは、「貨物を積載して走行するトラックの最大積載量に占める、実際に積載した貨物の量の割合」のことである。また、トラックの大きさ(最大積載量)は現状と取組案において全て同じである。 |
| 〇ア トラックの積載率は、取組案aとbのいずれにおいても改善される。 ×イ トラックの積載率は、取組案aでは改善されるが、bでは改善されない。 ×ウ トラックの積載率は、取組案bでは改善されるが、aでは改善されない。 ×エ トラックの積載率は、取組案aとbのいずれにおいても改善されない。 |
〃bは一瞬悩みますが、空車率が減るのでやはり積載率UPに。
この手は実際そうするしかないので、いちいち考えません。
POSデータ(リフト値)
これからのマーケターを名乗るには必須のリフト値。定義を覚えるより、何食わぬ顔でエクセル計算する方がずっと素早く身に付きます。
リフト値の解説はどのネットも動画もヘタクソ。そこに業を煮やしたChatGPTが解説し、以下を理解できないとAIに代替された元人類確定です。
| 支持度は、ある商品が購入された回数を、全体の購入履歴数で割った値です。例えば、1000回の購入履歴のうち、商品Aが600回購入された場合、支持度は 600 ÷ 1000 = 0.6 となります。 |
| 信頼度は、ある商品を購入した人のうち、ある別の商品も購入した人の数を、その商品を購入した人数で割った値です。例えば、商品Aを購入した人のうち、商品Bも購入した人が250人いた場合、商品Aを購入した人数が600人であれば、信頼度は 250 ÷ 600 = 5/12 となります。 |
| リフト値は、ある商品を購入した人のうち、ある別の商品も購入した人の割合が、その別の商品が全体の購入履歴に占める割合に比べてどれだけ高いかを示す指標です。具体的には、信頼度を、ある別の商品の支持度で割った値です。例えば、商品Aを購入した人のうち、商品Bも購入した人が50人で、商品Bの支持度が300人であれば、リフト値は (5/12) ÷ (3/10) = 25/18(正解〇オ) となります。リフト値が1より大きい場合、ある商品を購入した人の中で、ある別の商品も購入する確率が全体の購入履歴において期待される確率より高いことを示します。 |
この(設問1)は続く(〃2)で使うので、答を先に見て計算します。
| (設問1) | × | →〇 |
| ×ア | 95 | 0.42 (5/12) |
| ×ウ | 0.45 | 0.6 |
| ×エ | 57 | 0.83 (5/6) |
| ×オ | 0.35 | 0.3 |
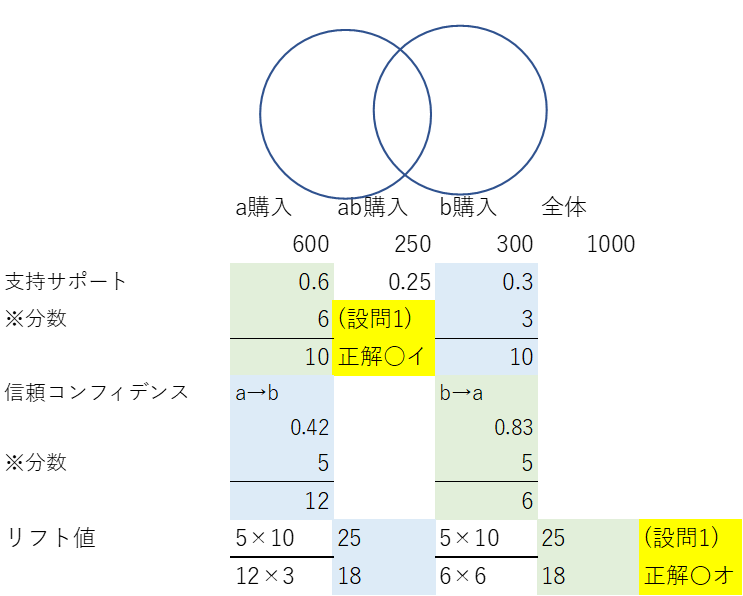
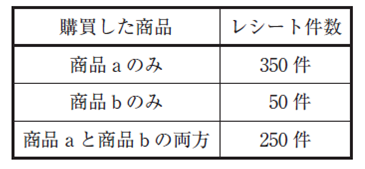
| ある小売店の一定期間におけるPOS システムから得られた1,000 件のレシートデータを分析する。このとき、商品aと商品bの購買パターンについて、下表のような結果が得られたとする。下記の設問に答えよ。 |
 |
| (設問1 ) 商品aと商品bの購買パターンについての評価指標に関する記述として、最も適切なものはどれか。 |
| (設問1 ) 商品aと商品bの購買パターンについての評価指標に関する記述として、最も適切なものはどれか。 ×ア 商品aからみた商品bの信頼度(コンフィデンス)は、95 である。 〇イ 商品aと商品bを併買したパターンの支持度(サポート)は、0.25 である。 ×ウ 商品aを購買したパターンの支持度(サポート)は、0.45 である。 ×エ 商品bからみた商品aの信頼度(コンフィデンス)は、57 である。 ×オ 商品bを購買したパターンの支持度(サポート)は、0.35 である。 |
リフト値は、(支持率サポート)÷(信頼度コンフィデンス)で求める。上記の分数をエクセルで自作しながら、正解〇オになると暗記完了です。
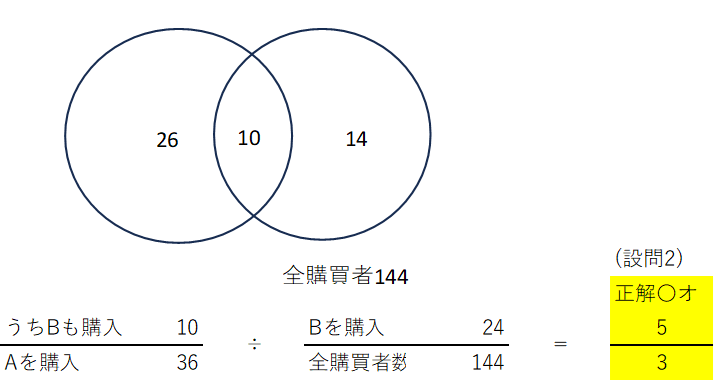
| (設問2 ) 商品aと商品bを併買した購買パターンのリフト値として、最も適切なものはどれか。 |
| ×ア 3/10 ×イ 5/13 ×ウ 5/9 ×エ 5/6 〇オ 25/18 |
リフト値を計算すると、【どの商品と併売されやすいか】のランキングを作成できる。さっそくエクセルで(Aを買ってBを買う率)÷(全員のうちBを買う率)を求めます。
| 次の文章を読んで、下記の設問に答えよ。 |
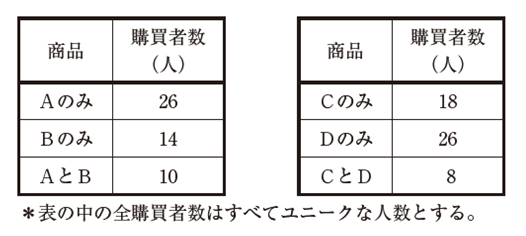
| 独自のオンラインサイトでネットショップを運営している、ある小売業の一定期間における顧客の購買状況を確認したところ、この期間におけるユニークな全購買者数は144人であった。 当該ネットショップの取り扱い商品のうち、A~Dの4 つの商品についてのみ考慮すると、その購買状況は下表のとおりであった。また、商品Aまたは商品Bを購買している顧客は、商品Cや商品Dの購買はなかったとする。この小売業では商品A~Dについて、全購買者数をベースとした商品購買における相関ルールを検討し、今後の商品プロモーションに活用したいと考えている。 |
 |
| (設問1 ) 以下の記述のうち、最も適切なものはどれか。 |
| ×ア 支持度(サポート)の値は、商品Aと商品Dで同じである。 ×イ 商品Aからみた商品Bの信頼度(コンフィデンス)は、商品Bからみた商品Aの信頼度(コンフィデンス)より大きい。 ×ウ 商品Aと商品Bのジャッカード係数は、商品Cと商品Dのジャッカード係数より小さい。 ○エ 商品Bの支持度(サポート)の値は、4 つの商品の中で最小である。 ×オ 商品Cからみた商品Dの信頼度(コンフィデンス)は、商品Dからみた商品Cの信頼度(コンフィデンス)より小さい。 |
| (設問2 ) 商品Aと商品Bを併買した購買パターンのリフト値として、最も適切なものはどれか。 |
| ×ア 1/4 ×イ 5/12 ×ウ 5/4 ×エ 3/2 ○オ 5/3 |
今日のまとめ
そして計算問題の出題論点は限られ、時間を取ってまとめて解けば類題ばかりで覚えやすい。ここに気付くと「事例Ⅲ」への不安が一気に減ります。