さあはじまりました、エコノミクスアワー。
待ちに待った日曜日、今日はインドア?それともアウトドア? おはようございます、Xレイでございます。
日曜日といいますと北海道民の朝は「それいけ!アンパンマン」から始まるわけでございます。子供はみんな大好きアンパンマン。私の子供も例外でなくさらには列車好きなものでして「アンパンマン列車に乗りたい!」と。少々前になりますが生まれて初めて四国へ行ってまいりました。
そうなりますと当然、高知県はアンパンマンミュージアムへ行きますよね。もちろんそこはアンパンマン好きの子供たちで大賑わい。顔色は皆同じ、幸せそうな楽しそうな時間を過ごしておりました。まあしかし、保護者サイドとなりますと様々な方々がいらっしゃいます。なかには少々強そうなといいますか、怖そうなといいますか、そのようなお父様もお見えになるわけです。アンパンマン、ジャムおじさん、バタコさん、名犬チーズと並んだオブジェがありまして、それを見たそのお父様
「ほら!○○。アンパンマンだぞ!」
普段、所属先ではアンパンマンなど口にすることはないのでしょうが、やはりここは可愛いお子様との大切な一時。親切にご案内しておりました。その次の瞬間
「ほら!その隣!ジャムおやじ!」
ん? ジャムおやじ?
やはり怖い・・・
といった話。
まあ、今日も元気100倍いってまいりましょう。
さて、経済学。
前々回、前回と生産者行動理論の等量曲線と等費用線、さらには簡単な費用最小化問題をみてきました。今日は関連の過去問、 平成29年第15問と平成30年第18問をやってみましょう。
まずは平成29年第15問。
第15問
下図には、等費用線が描かれている。この等費用線に関する記述として、最も適切なものを下記の解答群から選べ。
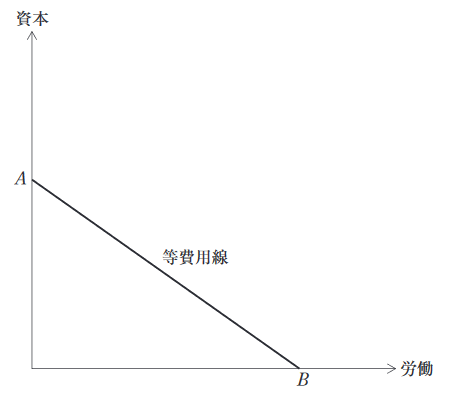
〔解答群〕
ア 資本のレンタル価格が上昇する場合、横軸上の切片Bは不変のままで、縦軸上の切片Aが上方に移動する。
イ 縦軸上の切片Aは、資本の最大投入可能量を示している。
ウ 賃金率が上昇する場合、横軸上の切片Bは不変のままで、縦軸上の切片Aが下方に移動する。
エ 費用が減少すると、等費用線は右方にシフトする。
それではいってみましょう。
選択肢ア。実はこの選択肢をみて前回後半の具体例(資本レンタル価格rの上昇)を選びました。そこでみたように「資本のレンタル価格が上昇する場合、横軸上の切片Bは不変のままで、縦軸上の切片Aが下方に移動する」というのが正しい。よって、選択肢アは誤り。ここは丸暗記ではなく、切片の式を頭に入れ考えて対応したいところです。
選択肢イ。等費用線は右下がりなので縦軸(資本)の値はグラフの左へいくほど大きくなる。設問の等費用線上で最も左にある点は切片A。つまり、資本の値はそこで最大値をとる。言い換えて「縦軸上の切片Aは、資本の最大投入可能量を示している」。よって、選択肢イは正しい。
選択肢ウ。賃金率が上昇する場合「横軸上の切片Bは左へ移動し、縦軸上の切片Aが不変のまま 」。よって、選択肢ウは誤り。選択肢アと考え方は全く同じ。繰り返し、切片の式から考えて対応したいところです。
選択肢エ。前回みたように「費用が減少すると、等費用線は左下へシフトする」。よって、選択肢エは誤り。「左下の等費用線ほど費用が小さい」これは絶対に覚えておきます。
以上より正解はイ。
平成29年第15問は、等費用線の基本的な知識、理解を問う問題でした。ただ、当時の診断士テキストでこの等費用線を扱っていたものはどのくらいありましたか?予算制約線をやっているからいいでしょ?と。まあまあ、こうなると次は等量曲線が間違いなく出題されますよね。それが早々次年度30年となるわけです。
その平成30年の第18問。
第18問
生産においては、生産要素を効率的に投入することが重要である。下図では、等産出量曲線と等費用線を用いて、最適な生産要素の投入量を考える。この図に基づいて、下記の設問に答えよ。
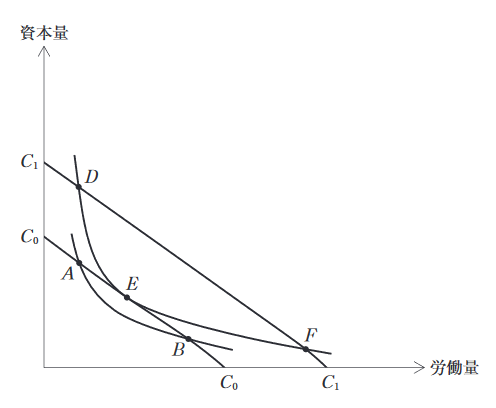
(設問 1 )
この図に関する記述として、最も適切なものはどれか。
ア 点Aと点Bは、労働と資本の投入による費用は同じであるが、生産量が異なる。
イ 点Dでは、労働と資本の投入による費用は点Bより少ないが、生産量は多くなっている。
ウ 点Fでは、点Dよりも資本の投入が少なく、労働の投入が多いので、費用が少なくてすむ。
エ 費用を一定とした場合、点Aでは、労働の投入を増加させ、資本の投入を減少させることによって、生産量が増加する余地がある。
(設問 2 )
この図においては、点Eで生産要素の最適投入が実現している。点Eに関する記述として、最も適切なものはどれか。
ア 点Eでは、点Bと同じ量を生産する場合の要素費用最小化が実現している。
イ 点Eでは、労働と資本について要素価格 1 単位当たりの限界生産物が均等化している。
ウ 点Eにおいては、点Aと技術的限界代替率が同じであるが、労働と資本の要素価格比率が異なっている。
エ 点Eにおける技術的限界代替率は、点Dと比べると大きく、点Fと比べると小さい。
まずは(設問1)いってみましょう。
選択肢ア。点Aと点Bは共に同じ等量曲線と等費用線上にある、つまり、点Aと点Bは費用も生産量も同じ。よって、選択肢アは誤り。
選択肢イ。点Dのある等費用線と点Bのある等費用線は平行で、点Dの等費用線の方が右上にある。つまり「点Dでは、労働と資本の投入による費用は点Bよりも多い」。よって、選択肢イは誤り。ちなみに「点Dの方が生産量が多い」というのは正しい
選択肢ウ。点Fと点Dは同じの等費用線上にあるので費用は同じ。よって、選択肢ウは誤り。ちなみに「点Fでは、点Dよりも資本の投入が少なく、労働の投入が多い」というのは正しい。
選択肢エ。少々日本語が分かりづらいですね。要するに、点Aと同じ費用で(労働の投入を増加させ、資本の投入を減少させることによって)生産量を増やせるかと。点Aは等量曲線と等費用線の接点となっていない。それは、より右上にある等量曲線とその等費用線が接し得るということ。つまり、点Aと同じ費用で生産量を増やせるということになる。なぜなら、右上にある等量曲線ほど生産量が多いから。具体的には点Eの生産量は点Aよりも多い。よって、選択肢Eは正しい。
以上より(設問1)の正解はエ。
(設問1)は等量曲線と等費用線とはどのようなものか知っていますか?という問題ですね。知っていれば簡単です。知っていれば(教わっていれば)ですけども。
次は(設問2)いってみましょう。
選択肢ア。 そもそも点Eと点Bの生産量は同じにならない。よって、選択肢アは誤り。
選択肢イ。結果この選択肢は正しいのですが、これは難しい。「加重限界生産力均等の法則」といいますが、それ知らなければ短時間で判断するのは相当難しい。まあ、やってみましょう。
「一方の生産要素を1単位増加させたとき、同じ生産量を保つために、もう一方の生産要素を何単位減少させるべきかを示したもの」
本設問に合わせて前者を労働投入量、後者を資本投入量として言い換えると
「労働投入量を1単位増加させたとき、同じ生産量を保つために、資本投入量を何単位減少させるべきかを示したもの」
要するに、同じ生産量を保つための労働投入量と資本投入量の交換レートといった感じでしょうか。これを定式化にすると
技術的限界代替率=(資本の減少量)/(労働の増加量)
と表せます。
余談ですが、これは中学数学の関数で出てくる「変化の割合」の概念に近いです。ただし分子分母を「変化量」でなく「減少量」と「増加量」と特定し、技術的限界代替率の符号をあえてプラスにしている点に注意です。この先「絶対値」という言葉が何度か出てくるのはこのため。個人的には、符号と言葉の使い方がややこしく感じます。別段マイナスで議論してもよさそうなのに。負の傾きの大小を嫌いましたか。
話を戻して、上式右辺の分子分母に(生産量)/{(資本の減少量)×(労働の増加量)}をかけてみます。すると
分子=(生産量)/(労働の増加量)
分母=(生産量)/(資本の減少量)
となります。この分子と分母は各々「労働の限界生産力」と「資本の限界生産力」を表していて
技術的限界代替率=(労働の限界生産力)/(資本の限界生産力)・・・①
とすることができます。この辺りの式の変形が難しければ、とりあえず①式の結果だけをおさえて「ああ、そうなんですか」と進みましょう。
さておきまして、等量曲線上のある点におけるこの技術的限界代替率。グラフではその点を通る「接線の傾きの絶対値」で表されます。
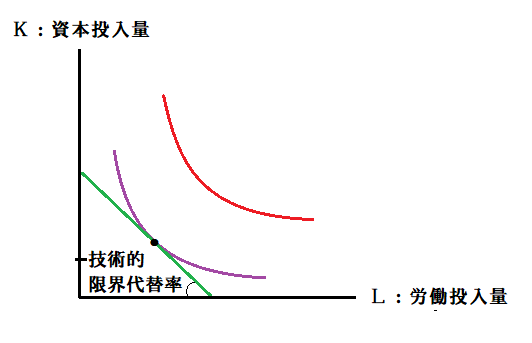
その理由は数学の極限、微分が分からないと厳しいので、難しければここもそういうものかと進みましょう。
一方で、前回みたように等費用線の傾きの絶対値は、「労働1単位当たりの賃金」と「資本1単位当たりのレンタル価格」の比で表されます。式にして
等費用線の傾きの絶対値=(労働1単位当たりの賃金:w)/(資本1単位当たりのレンタル価格:r)・・・②
ということです。また「費用最小化が実現」しているとき、等費用線と等量曲線は接しています。
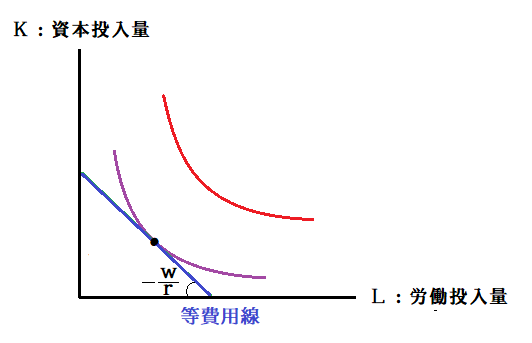
よって、「費用最小化が実現」しているとき、等費用線はこのように表されます。
さてここで、 上の2つのグラフをみてみると「費用最小化が実現」しているとき【技術的限界代替率=等費用線の傾きの絶対値】となることが分かります。つまりこのとき①式=②式が成り立ち
(労働の限界生産力)/(資本の限界生産力)=(労働1単位当たりの賃金)/(資本1単位当たりのレンタル価格)・・・③
と表すことができます。実はこの③式が費用最小化の条件ともいえるのです。そして③式の両辺に(資本の限界生産力)/(労働1単位当たりの賃金)をかけると
(労働の限界生産力)/(労働1単位当たりの賃金)=(資本の限界生産力)/(資本1単位当たりのレンタル価格)・・・④
と変形できます。この④式の示す内容こそが、選択肢イ「労働と資本について要素価格 1 単位当たりの限界生産物が均等化している」と同義です。
そして④式が成り立つ条件として「費用最小化の実現」が必要でした。本設問の点Eはその条件を満たしている。よって、選択肢イは正しいといえるのです。
「加重限界生産力均等の法則」。割ときれいに導いたつもりですがどうでしょう。
選択肢ウ。上記解説を参考にして「点Eにおいては、点Aと技術的限界代替率は異なっているが、労働と資本の要素価格比は同じとなっている」。よって、選択肢ウは誤り。
選択肢エ。これも上記解説を参考にして、 技術的限界代替率の大小はグラフで切片の傾きの絶対値で考えると分かりやすい。各点の技術的限界代替率は【点D>点E>点F】となっている。選択肢エの示す内容は【点F>点E>点D】なので全く逆。よって、選択肢エは誤り。
以上より(設問2)の正解はイ。
(設問2)は、繰り返し選択肢イの内容が難しい。昨年正解された方の多くは消去法でしたでしょうか。
平成30年第18問は、生産者行動理論の等量曲線と等費用線。さすがにお手持ちの今年度版テキスト、教材では扱っていますか?この辺りをしっかりやらずにいきなり生産関数をぶち込むからよく分からない。そう思っていましたけども。
まあ、これくらいにしておきましょう。さて、私の寄稿も一旦今回でお終いですが、1次試験前にもう一度だけ登場する予定です。そこでは過去問を中心に生産関数をやりましょう。
それでは、また。
Xレイ
■■ここからテンプレ■■
