【無理を言ってお願いシリーズ】

ブログを一人で書けば首尾一貫。ところが診断士の良い点は、多様な意見が交わり、そこから議論が発展することです。「経済学」を暗記で解いてはつまらない。そこで無理を言って寄稿をお願いした【エコノミクスアワー】ですが、いきなり誰もが苦手な「生産関数」。ではXレイ様、よろしくお願いします。
【Xレイ】ミクロ経済学 等量曲線
ブログ読者の皆様、はじめまして Xレイ と申します。
何者かと申しますと、主ふうじんさんとはこちらのブログで先輩後輩の間柄、私が5期後輩でございます。まあ、そちらのコミュニティでは私などすでに幽霊部員。このところの執筆陣には「誰だお前?」と言われること間違いなく、まったく存在感はございません。そんな私に「久々にブログでも書いてみたら?」とのお声掛け、お応えすべくこうして登場してまいりました。
といったわけでいってみましょう、エコノミクスアワー。
週の真ん中水曜日、今日のご機嫌いかがでしょうか。
改めまして、Xレイ でございます。
近況ですが3カ月ほど前に怪我をしました。右示指伸筋腱の皮下断裂。
マレットフィンガーと呼ばれるもので、DIP関節(第1関節)を自力で伸ばせなくなるのですが、幸い痛みはそれほどでもございません。ただこれ、骨折していると相当厄介だったんですね。まあ、私の場合は大丈夫、何とか保存療法ですみました。
怪我の原因は些細なことでして。5歳の息子がいるのですが、この年頃、戦いごっこは欠かせません。もちろん仮面ライダーですよね。息子はジクウドライバーを持っていますので仮面ライダージオウ、さらにはビルドウォッチでアーマータイム、ビルドアーマーとなるわけです。
ならば私は当然アナザービルド、最終的にはやられる運命にございます。「勝利の法則は決まった!」とのやられ際、息子の腰付近に手を伸ばしたところ、突進されてジクウドライバーに指を突き腱断裂。いや~ジクウドライバーはなかなか固い!といった話・・・
まあ、試験にむけてこのような怪我にも気を付けましょう!
と上手くまとめて本題でございます。
さて、経済学。
今日はミクロ経済学の生産者行動理論。
何かを生産するためには、例えば、労働、資本(機械や建物と捉えてO.K.)、土地といった「生産するためのもの」が必要です。この「生産するためのもの」のことを「生産要素」といいます。それでは、その生産要素を使う量すなわち「生産要素投入量」とそれを使って生産できる「生産量」との関係はどうなっているのか。
まあ、「生産要素投入量」が増えると「生産量」も増えそうだというところまでは想像できますが、いったいどのような関係(法則、ルール)に従って「生産量」が決まっていくのか。その関係(法則、ルール)を表すのが、皆様苦手な「生産関数」というわけです。
数学的に言い換えると、「生産要素投入量」の値が決まると何らかの関係に従って「生産量」の値が1つに決まる。このような関係にあるとき「生産量」は「生産要素投入量」の関数であるといい、その関数を経済学では「生産関数」と呼んでいると。
そんなことはいいからと怒られそうですが、いやいや、まずはこのようなことからしっかりとおさえる。こちらにも書いてあるようなこと。経済学に限らず何かを学ぶとき、まずはこのような根本的なところをしっかりとおさえることが重要と思っています。
話を戻して「生産要素」。
先ほどは例として労働、資本、土地をあげました。経済学の議論では、そのうち「労働」と「資本」2つの生産要素を使って生産すると仮定することが多いです。土地やその他要素を加えると話がややこしくなるからでしょう。何だか非現実的との批判もあるでしょうが、こういう議論はまずモデルをできるだけ簡素に確立し、そこに必要なものを加えて発展させていけばいいんです。さておきまして、そのように「生産量」が「労働投入量」と「資本投入量」の関数である場合、
〔Y:生産量 L:労働投入量 K:資本投入量〕
と一般的に表されます。
もう少し具体的に、労働と資本ともに限界生産力が低減するという仮定の下、
〔A:技術水準(全要素生産性) a:労働分配率 b:資本分配率〕
という関数を使うことも多いです。これが「コブダグラス型生産関数」です。 数学嫌いの方にはそろそろ逃げ出されそうですが、この辺りの式はとりあえず分からなくても大丈夫。そんなもんですかと進みましょう。逆に、このような話をもっと詳しくという方は、こちらの前半でどうでしょう。リンク先、かなり気合いを入れて書いていますので、経済学で100点をという方はどうぞ。
話は戻って、そのコブダグラス型生産関数をグラフで表すと、どのようになるのか分かりますか?
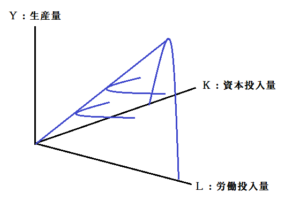
一例としてこのような形になります。ここで注目してもらいたいのはその形状ではなく次元、立体的に表されるという点です。この関数は、2つの独立変数L、Kによって従属変数Yが決まるという3次元関数だからです。
この先いろいろな分析を、もちろんこの3次元のグラフを使って行うのもいいでしょう。しかし、3次元のグラフというのは非常に扱いづらい。ならば
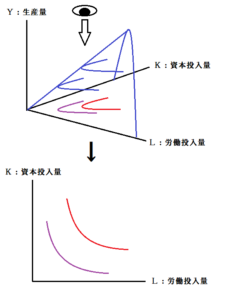
このようにして、あたかも上から投影して見たかのように、等しい生産量ごとに2次元化して描いてみてはどうかと。改めましてこちら。
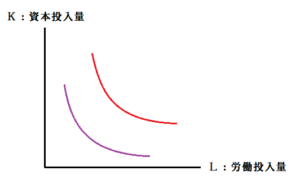
紫と赤、各々の曲線は何を表しているかというと、等しい生産量となるような労働投入量Lと資本投入量Kの組合せ。言い換えて「同じ生産量を生産するのに必要な労働投入量Lと資本投入量Kの組合せ」を表しています。
これが「等量曲線(等生産量曲線)」です。
労働投入量Lと資本投入量Kの増加は生産量を増やすので、右上の等量曲線ほど生産量は多くなります。上のグラフでは、紫よりも赤の曲線上の点の方が生産量が多いということです。
そして昨年度、平成30年第18問のグラフの曲線がまさしくこの等量曲線。今日の段階でとりあえず、(設問1)選択肢アは間違いということが分かったと思います。その問題のように、ここに「等費用線」を描いて費用最小化条件を考えていくのですが、続きは次回。
今日は、3次元の生産関数から等量曲線に至るまでのお話。この内容はいつかやりたいと思っていました。というのは、苦手な方が多い「生産関数」、多くのテキストではおそらく1生産要素の話から入っていますか。これ、今回のところから始めて、次に労働か資本のどちらかを固定するといった捉え方で1生産要素に移った方がうまくいくような気がするんですよね。
まあ、確かに入り口部分は難しくはなりますが。でも、消費者行動理論は無差別曲線から入っているわけで。それならこれでいいのかなって。どうせマクロではやるんですよね、コブダグラス型。
と、まあ、個人的見解ですが。それでは、また。
Xレイ
■■ここからテンプレ■■